I see a lot of data scientists using tests such as the Shapiro-Wilk test and the Kolmogorov–Smirnov to test for normality. Stop doing this. Just stop. If you’re not yet convinced (and I don’t blame you!), let me show you why these are a waste of your time.
Why do we care about normality?
We should care about normality. It’s an important assumption that underpins a wide variety of statistical procedures. We should always be sure of our assumptions and make efforts to check that they are correct. However, normality tests are not the way for us to do this.
However, in large samples (n > 30) which most of our work as data scientists is based upon the Central Limit Theorem usually applies and we need not worry about the normality of our data. But in cases where it does not apply let’s consider how we can check for normality in a range of different samples.
Normality testing in small samples
First let us consider a small sample. Say n=10. Let’s look at the histogram for this data.
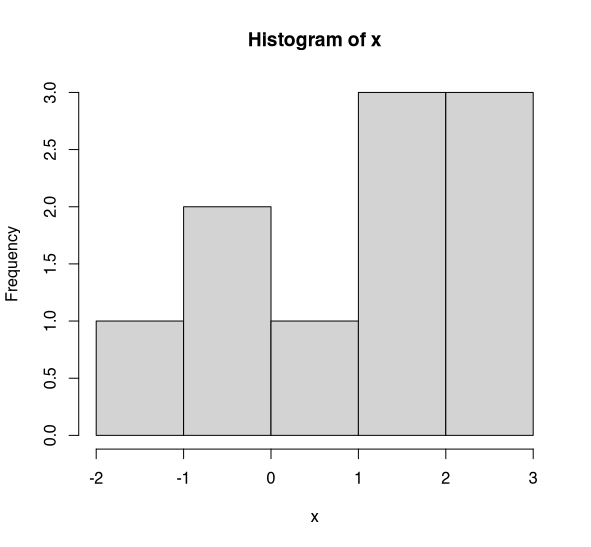
Histogram of x (n=10). (Image by author)
Is this normally distributed? Doesn’t really look like it — does it? Hopefully you’re with me and accept that this isn’t normally distributed. Now let’s perform the Shapiro-Wilk test on this data.
Oh. p=0.53. No evidence to suggest that x is not normally distributed. Hmm. What do you conclude then. Well, of course, not being evidence that x is not normally distributed does not mean that x is normally distributed. What’s actually happening is that in small samples the tests are _underpowered _to detect deviations from normality.

Normal Q-Q Plot of x (n=10). (Image by author)
The best way to assess normality is through the use of a quantile-quantile plot — Q-Q plot for short. If the data is normally distributed we would expect to see a straight line. This data shows some deviation from normality, the line is not very straight. There appears to be some issues in the tail. Admittedly, without more data it is hard to say.
With this data, I would have concerns about assuming normality as there appears to be some deviation in the Q-Q plot and in the histogram. But, if we had just relied on our normality test, we wouldn’t have picked this up. This is because the test is underpowered in small samples.
Normality testing in large samples
Now let’s take a look at normality testing in a large sample (n=5000). Let’s take a look at a histogram.

Histogram of x (n=5000). (Image by author)
I hope you’d all agree that this looks to be normally distributed. Okay, so what does the Shapiro-Wilk test say. Bazinga! p=0.001. There’s very strong evidence that x is not normally distributed. Oh dear. Well, let’s take a quick look at our Q-Q plot. Just to double check.
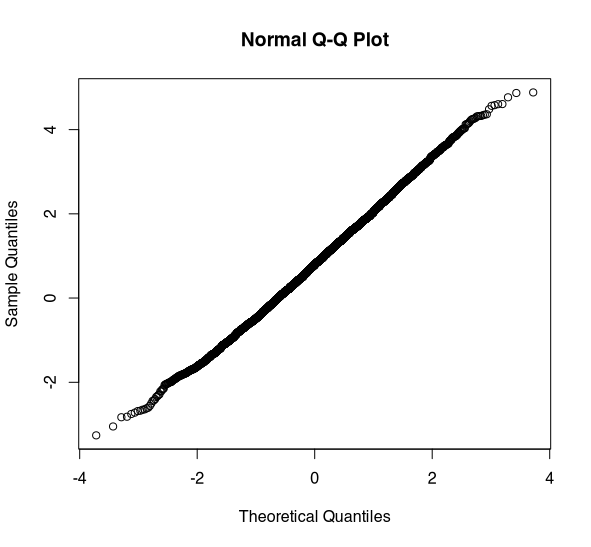
Normal Q-Q plot for x (n=5000). (Image by author)
Wow. This looks to be normally distributed. In fact, there shouldn’t be any doubt that this is normally distributed. But, the Shapiro-Wilk test says it isn’t.
What’s going on here? Well the Shapiro-Wilk test (and other normality tests) are designed to test for theoretical normality (i.e. the perfect bell curve). In small samples these tests are underpowered to detect quite major deviations from normality which can be easily detected through graphical methods. In larger samples these tests will detect even extremely minor deviations from theoretical normality that are not of practical concern.
Conclusion
Hopefully, I have shown you that normality tests are not of practical utility for data scientists. Don’t use them. Forget about them. At best, they are useless; at worst, they are misleading. If you want to assess the normality of some data, use Q-Q plots and histograms. They’ll give you a much clearer picture about the normality of your data.
#normal-distribution #statistics #tests-of-normality #mathematics #data-science