Dynamic programming is a technique for solving problems, whose solution can be expressed recursively in terms of solutions of overlapping sub-problems. A gentle introduction to this can be found in How Does DP Work? Dynamic Programming Tutorial.

This lesson was originally published at https://algodaily.com, where I maintain a technical interview course and write think-pieces for ambitious developers.

Memoization is an optimization process. In simple terms, we store the intermediate results of the solutions of sub-problems, allowing us to speed up the computation of the overall solution. The improvement can be reduced to an exponential time solution to a polynomial time solution, with an overhead of using additional memory for storing intermediate results.

Let’s understand how dynamic programming works with memoization with a simple example.

Fibonacci Numbers

You have probably heard of [**Fibonacci numbers**](https://algodaily.com/challenges/fibonacci-sequence/) several times in the past, especially regarding recurrence relations or writing recursive functions. Today we’ll see how this simple example gives us a true appreciation of the power of dynamic programming and memoization.

Definition of Fibonacci Numbers

The nth Fibonacci number f(n) is defined as:

f(0) = 0                                       // base case
f(1) = 1                                       // base case 
f(n) = f(n-1) + f(n-2)    for n>1              // recursive case

The sequence of Fibonacci numbers generated from the above expressions is:

0 1 1 2 3 5 8 13 21 34 ...

Pseudo-code for Fibonacci Numbers

When implementing the mathematical expression given above, we can use the following recursive pseudo-code attached.

Routine: f(n)
Output: Fibonacci number at the nth place

Base case:
1\. if n==0 return 0
2\. if n==1 return 1
Recursive case:
1\. temp1 = f(n-1)
2\. temp2 = f(n-2)
3\. return temp1+temp2

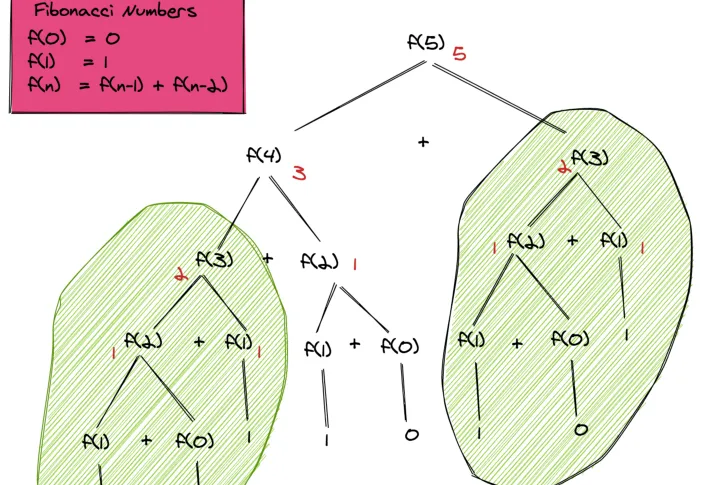
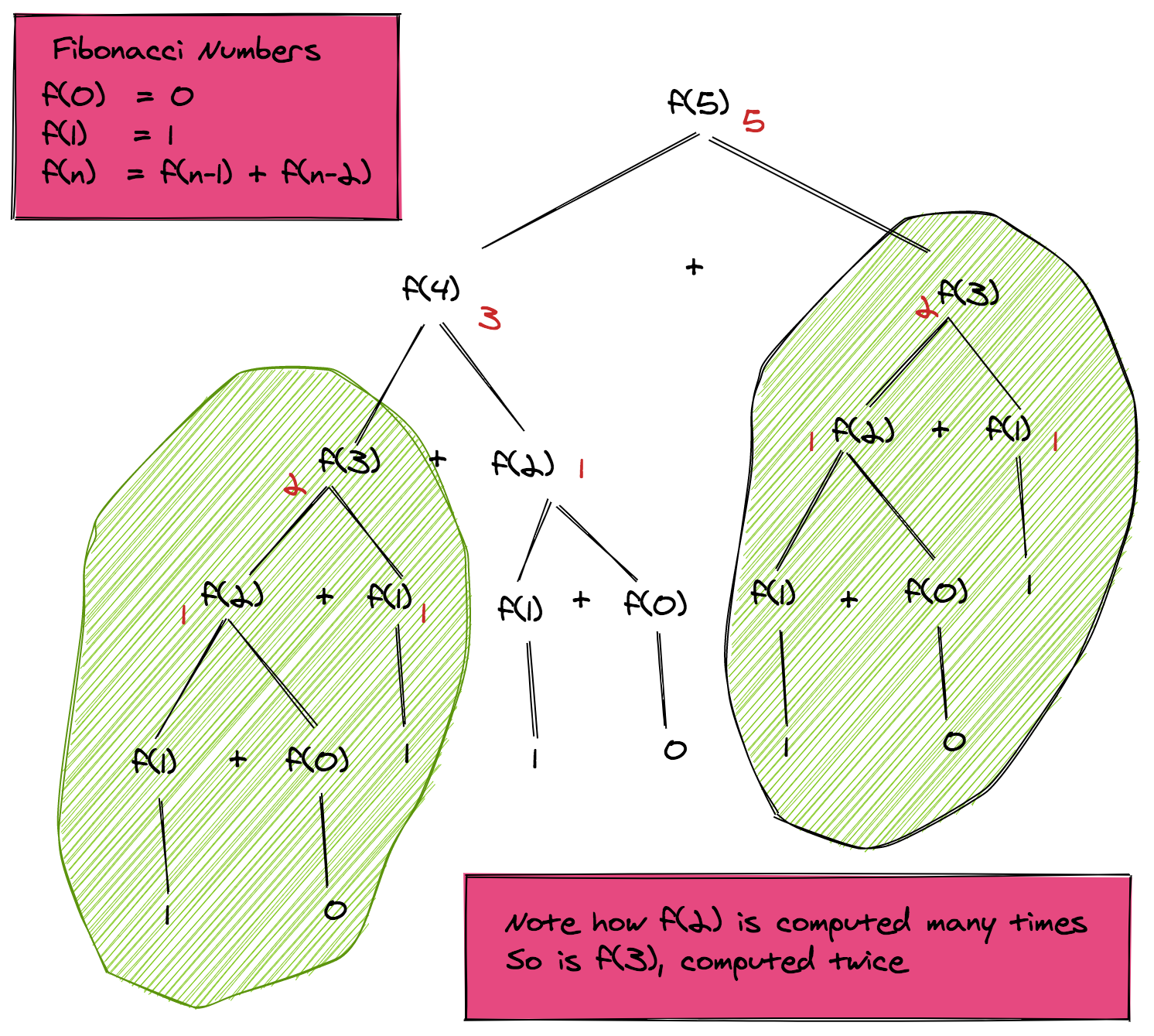
The recursion tree shown below illustrates how the routine works for computing f(5) or fibonacci(5).

If we look closely at the recursive tree, we can see that the function is computed twice for f(3), thrice for f(2) and many times for the base cases f(1) and f(0). The overall complexity of this pseudo-code is therefore exponential O(2n). We can very well see how we can achieve massive speedups by storing the intermediate results and using them when needed.

Memoization of Fibonacci Numbers: From Exponential Time Complexity to Linear Time Complexity

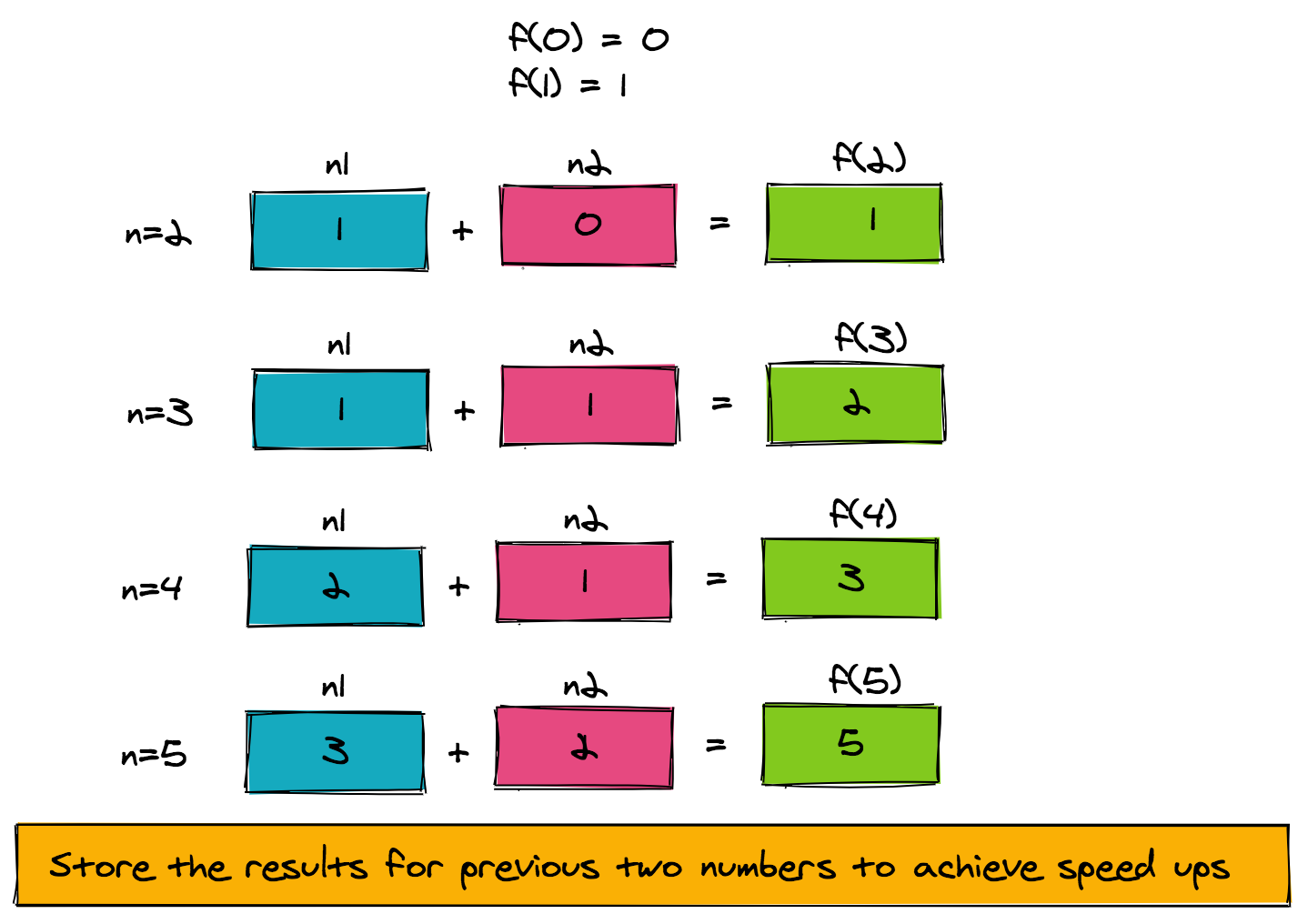
To speed things up, let’s look at the structure of the problem. f(n) is computed from f(n-1) and f(n-2). As such, we only need to store the intermediate result of the function computed for the previous two numbers. The pseudo-code to achieve this is provided here.

The figure below shows how the pseudo-code is working for f(5). Notice how a very simple memoization technique that uses two extra memory slots has reduced our time complexity from exponential to linear (**O(n)**).

Routine: fibonacciFast
Input: n
Output: Fibonacci number at the nth place
Intermediate storage: n1, n2 to store f(n-1) and f(n-2) respectively
1\. if (n==0) return 0
2\. if (n==1) return 1
3\. n1 = 1
4\. n2 = 0
5\. for 2 .. n
    a. result = n1+n2           // gives f(n)
    b.   n2 = n1                // set up f(n-2) for next number
    c.   n1 = result            // set up f(n-1) for next number
6\. return result

Maximizing Rewards While Path Finding Through a Grid

Now that we understand memoization a little better, let’s move on to our next problem. Suppose we have an m * n grid, where each cell has a “reward” associated with it. Let’s also assume that there’s a robot placed at the starting location, and that it has to find its way to a “goal cell”. While it’s doing this, it will be judged by the path it chooses. We want to get to the “goal” via a path that collects the maximum reward. The only moves allowed are “up” or “right”.

#data-structures #computer-science #software-development #dynamic-programming #algorithms #algorithms