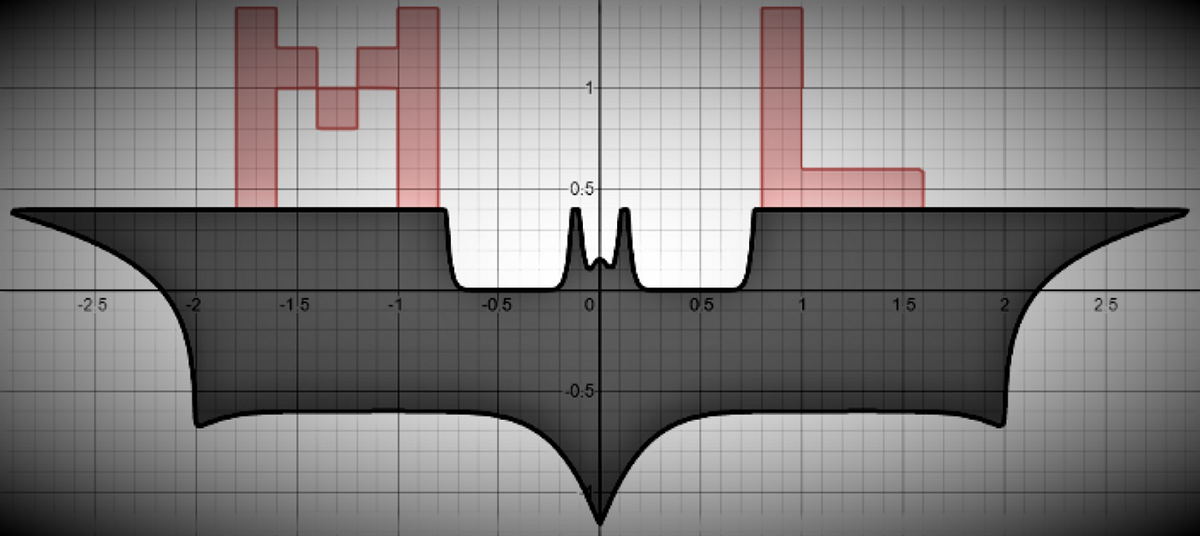
Introduction:
The circle in itself is really pretty, ain’t it? But, with some curiosity, you can go beyond a circle. It doesn’t need any calculus or any advanced concepts, just with our favourite class 10 mathematics and with some beautiful ideas, we can go beyond the circle and even create the Batman Inequation. This article is about creating inequations for whatever shapes we want. In the second part, we will see how we can improve and generalize this framework and derive commonly used functions in Machine Learning.

This is a journey from the curve on the left to the one on the right
All visualisations created here are generated in openly available software like Desmos and Geogebra. I suggest the readers go ahead and play with these equations using these tools and explore the beauty by themselves.
The potential of a Circle!
The humble circle describes multiple points which lie equidistant from a given centre point. Let’s have a look at our familiar friend in all its forms. When all points lie at a given distance, let’s consider 1 unit, we get a circle. Points with distance less than 1 lie inside the circle and ones with more than 1 lie outside the circle. In 3 dimensions a paraboloid with the equation z=x²+y²–1 forms our circle when it intersects with the XY plane.
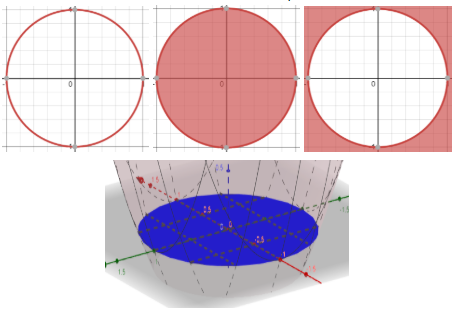
Different views of a circle
We all know that a circle normally takes the form x²+y²=1. What do you think will happen if we go beyond the power of 2? That’s where the magic lies. Let’s take the values from 2 to 10 and observe what happens.
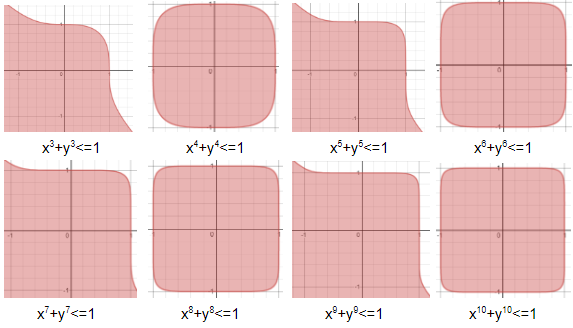
Powers going from 3 to 10
For even powers, we see the circle starts looking like a square and it does become one at infinite power. But why does it do so and especially at even powers? We will first try to understand how the points lying on the curve (x^n+y^n=1) behave and then look into the nature and properties of points within the curve (x^n+y^n<=1).
#machine-learning #mathematics #beautiful-things #creativity #art #deep learning