Photo by Scott Webb from Pexels

Linear Regression is one of the fundamental supervised-machine learning algorithm. While it is relatively simple and might not seem fancy enough when compared to other Machine Learning algorithms, it remains widely used across various domains such as Biology, Social Sciences, Finance, Marketing. It is extremely powerful and can be used to forecast trends or generate insights.Thus, I simply cannot emphasize enough how important it is to know Linear Regression — its working and variants — inside out before moving on to more complicated ML techniques.

---

Linear Regression Models are extremely powerful and can be used to forecast trends & generate insights.

---

The objective of the article is to provide a comprehensive overview of linear regression model. It will serve as an excellent guide for last-minute revisions or to develop a mindmap for studying Linear Regression in detail.

Note: Throughout this article, we will work with the popular Boston Housing Dataset which can be imported directly in Python using sklearn.datasets or in R using the library MASS(Modern Applied Statistics Functions). The code chunks are written in R.

What is Linear Regression?

Linear Regression is a statistical/machine learning technique that attempts to model the linear relationship between the independent predictor variables X and a dependent quantitative response variable Y. It is important that the predictor and response variables be numerical values. A general linear regression model can be represented mathematically as

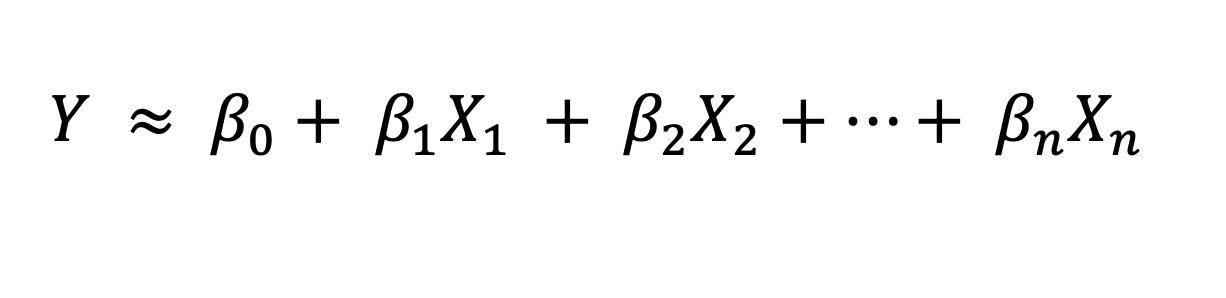
Linear Regression Model Equation; Image by Author

Since the linear regression model** approximates** the relationship between Y and X, by capturing the irreducible error term we get

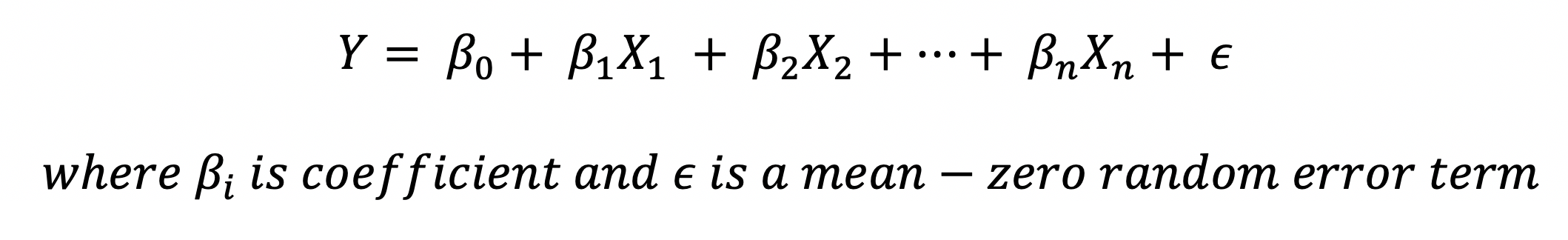
Linear Regression Model Equation with Approximation; Image by Author

Here, we will use Linear Regression to predict Median House Value (Y/response variable = medv)for 506 neighborhoods around Boston.

What insights does Linear Regression reveal?

Using Linear Regression to predict median house values will help answer the following five questions:

1. Is there a linear relationship between the predictor & response variables?
2. Is there an association between the predictor & response variables? How strong?
3. How does each predictor variable effect the response variable?
4. How accurate is the prediction of response variable?
5. Is there any interaction among the independent variable?

#machine-learning #data-science #data-science-interview #linear-regression #towards-data-science