Preface

In part 1 of this series (Linear Equation as a Neural Network building block) we saw what linear equations are and also had a glimpse of their importance in building neural nets.

In part 2 (Linear equation in multidimensional space) we saw how to work with linear equations in vector space, facilitating us to work with many variables.

Now I will show you how one linear equation can be embedded into another one (mathematically this is known as Function Composition) to structure a neural network. I will then proceed with how linear combination of weight matrices and feature vectors can help us with all the maths involved in the feed forward pass, ending this story with a working example.

This series has a mantra (note of comfort) that I will repeat below in case the eventual reader hasn’t read part 1.

Mantra: A note of comfort to the eventual reader

I won’t let concepts like gradient and gradient descent, calculus and multivariate calculus, derivatives, chain rule, linear algebra, linear combination and linear equation become boulders blocking your path to understanding the math required to master neural networks. By the end of this series, hopefully, these concepts will be perceived by the reader as the powerful tools they are and how they are simply applied to building neural networks.

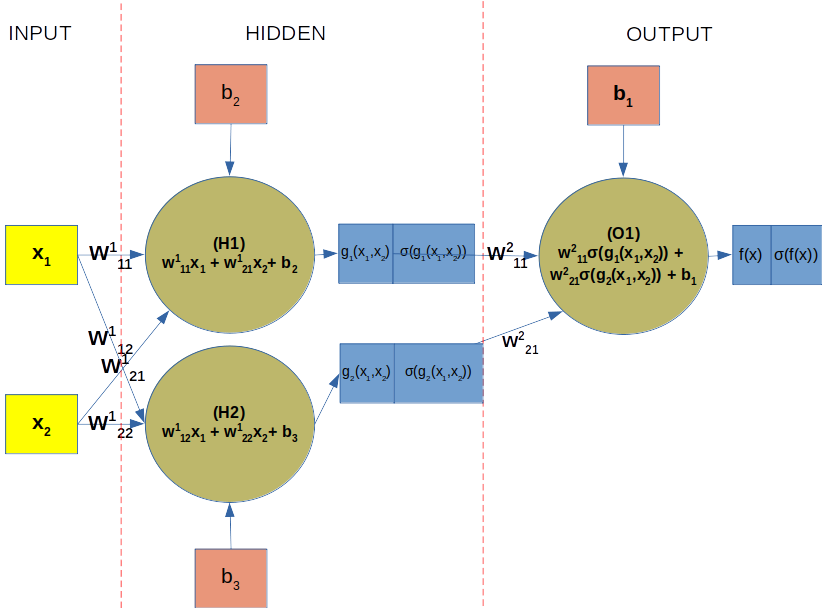
Function composition

If linear equations are neural networks’s building blocks, function composition is what binds them. Great! But what is function composition?

Lets consider the 2 linear equations below:

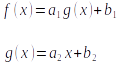
Equation 1: Function composition

What is different here? The difference is that in order to calculate the value of f(x), for any given**_ x_**, we first need to compute the value of g(x). This simple concept is known as function composition.

The above definition and notation, although correct, are not the ones commonly used. Function composition is normally defined as an operation where the result of function g(x) is applied to function f(x), yielding in a function h(x). Thus: h(x) = f(g(x)). **Another notationis: **(f ∘g)(x)=f(g(x)). And the above equations are written as follows:

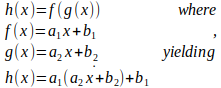
Equation 2: h(x) written as a composition of f(x) and g(x)

Schematically the above function composition can drawn as illustrated in figure 1.

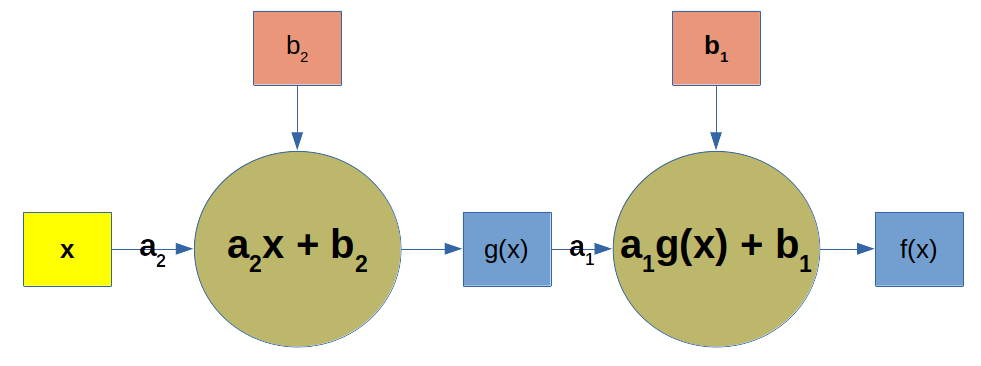
Figure 1: Function composition described as a network

In the above picture x is the input, or the independent variable. This input is multiplied by the angular coefficient _a_₂ which added to _b_₂ yields g(x). In turn, g(x) is multiplied by **_a₁, _**then added to b₁ resulting in f(x).

I find this really cool! Aren’t we getting closer to a neural network?

Believe me. If you understood what these two concepts (linear equation and function composition) are, you understood mathematically 80% of what a feed forward neural network is. What remains is to understand how to add additional independent variables (x₁, x₂, …, xₙ) to enable our neural network to work with many (probably the majority) of real world problems one deals with.

#neural-networks #multilayer-perceptron #feed-forward #perceptron #neural networks