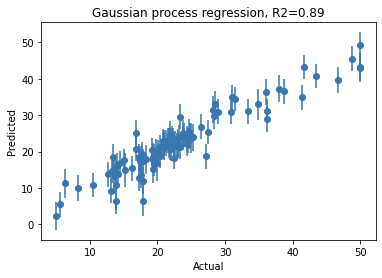
Gaussian processing (GP) is quite a useful technique that enables a non-parametric Bayesian approach to modeling. It has wide applicability in areas such as regression, classification, optimization, etc. The goal of this article is to introduce the theoretical aspects of GP and provide a simple example in regression problems.

Multivariate Gaussian distribution

We first need to do a refresher on multivariate Gaussian distribution, which is what GP is based on. A multivariate Gaussian distribution can be fully defined by its mean vector and covariance matrix

There are two important properties of Gaussian distributions that make later GP calculations possible: marginalization and conditioning.

Marginalization

With a joint Gaussian distribution, this can be written as,

We can retrieve a subset of the multivariate distribution via marginalization. For example, we can marginalize out the random variable Y, with the resulting X random variable expressed as follows,

Note that the marginalized distribution is also a Gaussian distribution.

Conditioning

Another important operation is conditioning, which describes the probability of a random variable given the presence of another random variable. This operation enables Bayesian inference, as we will show later, in deriving the predictions given the observed data.

#gaussian-process #scikit-learn #regression #gaussian-distribution #bayesian-inference #deep learning