SciPy Cheat Sheet: Linear Algebra in Python
This Python cheat sheet is a handy reference with code samples for doing linear algebra with SciPy and interacting with NumPy.
By now, you will have already learned that NumPy, one of the fundamental packages for scientific computing, forms at least for a part the fundament of other important packages that you might use used for data manipulation and machine learning with Python. One of those packages is SciPy, another one of the core packages for scientific computing in Python that provides mathematical algorithms and convenience functions built on the NumPy extension of Python.
You might now wonder why this library might come in handy for data science.
Well, SciPy has many modules that will help you to understand some of the basic components that you need to master when you’re learning data science, namely, math, stats and machine learning. You’ll see that for statistics, for example, a module like scipy.stats, etc. will definitely be of interest to you.
The other topic that was mentioned was machine learning: here, the scipy.linalg and scipy.sparse modules will offer everything that you’re looking for to understand machine learning concepts such as eigenvalues, regression, and matrix multiplication…
But, what is maybe the most obvious is that most machine learning techniques deal with high-dimensional data and that data is often represented as matrices. What’s more, you’ll need to understand how to manipulate these matrices.
That is why DataCamp has made a SciPy cheat sheet that will help you to master linear algebra with Python.
Take a look by clicking on the button below:
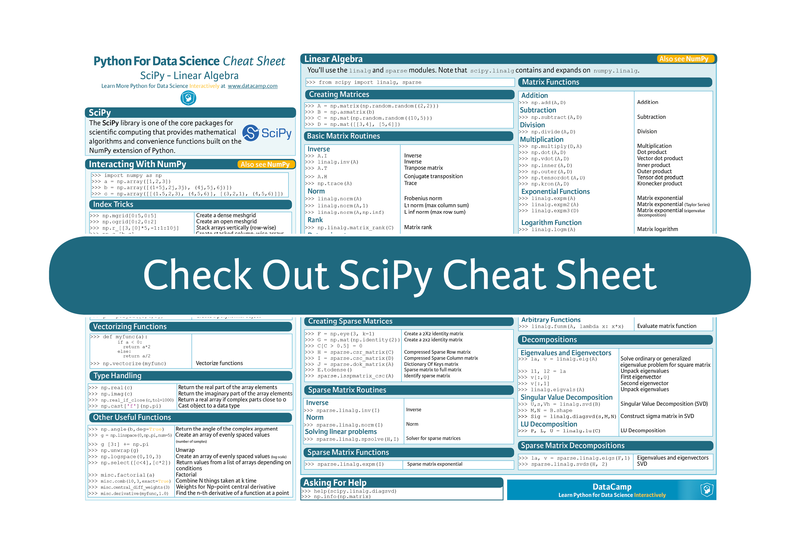
You’ll see that this SciPy cheat sheet covers the basics of linear algebra that you need to get started: it provides a brief explanation of what the library has to offer and how you can use it to interact with NumPy, and goes on to summarize topics in linear algebra, such as matrix creation, matrix functions, basic routines that you can perform with matrices, and matrix decompositions from scipy.linalg. Sparse matrices are also included, with their own routines, functions, and decompositions from the scipy.sparse module.
(Above is the printable version of this cheat sheet)
Python for Data-Science Cheat Sheet: SciPy - Linear Algebra
SciPy
The SciPy library is one of the core packages for scientific computing that provides mathematical algorithms and convenience functions built on the NumPy extension of Python.
Asking For Help
>>> help(scipy.linalg.diagsvd)
Interacting With NumPy
>>> import numpy as np
>>> a : np.array([1,2,3])
>>> b : np.array([(1+5j,2j,3j), (4j,5j,6j)])
>>> c : np.array([[(1.5,2,3), (4,5,6)], [(3,2,1), (4,5,6)]])
Index Tricks
| >>> np.mgrid[0:5,0:5] | Create a dense meshgrid |
| >>> np.ogrid[0:2,0:2] |
| >>> np.r_[3,[0]*5,-1:1:10j] | Stack arrays vertically (row-wise) |
| >>> np.c_[b,c] |
Shape Manipulation
| >>> np.transpose(b) | Permute array dimensions |
| >>> b.flatten() | Flatten the array |
| >>> np.hstack((b,c)) | Stack arrays horizontally (column-wise) |
| >>> np.vstack((a,b)) | Stack arrays vertically (row-wise) |
| >>> np.hsplit(c,2) | Split the array horizontally at the 2nd index |
| >>> np.vpslit(d,2) |
Polynomials
| >>> from numpy import poly1d |
| >>> p : poly1d([3,4,5]) | Create a polynomial object |
Vectorizing Functions
| >>> def myfunc(a): |
| if a ‹ 0: |
| return a*2 |
| else: |
| return a/2 |
| >>> np.vectorize(myfunc) | Vectorize functions |
Type Handling
| >>> np.real(b) | Return the real part of the array elements |
| >>> np.imag(b) | Return the imaginary part of the array elements |
| >>> np.real_if_close(c,tol:1000) | Return a real array if complex parts close to 0 |
| >>> np.cast['f'](np.pi) | Cast object to a data type |
Other Useful Functions
| >>> np.angle(b,deg:True) | Return the angle of the complex argument |
| >>> g : np.linspace(0,np.pi,num:5) | Create an array of evenly spaced values (number of samples) |
| >>> g [3:] +: np.pi |
| >>> np.unwrap(g) |
| >>> np.logspace(0,10,3) | Create an array of evenly spaced values (log scale) |
| >>> np.select([c<4],[c*2]) | Return values from a list of arrays depending on conditions |
| >>> misc.factorial(a) | Factorial |
| >>> misc.comb(10,3,exact:True) | Combine N things taken at k time |
| >>> misc.central_diff_weights(3) | Weights for Np-point central derivative |
| >>> misc.derivative(myfunc,1.0) | Find the n-th derivative of a function at a point |
Linear Algebra
You’ll use the linalg and sparse modules. Note thatscipy.linalg contains and expands onnumpy.linalg.
| >>> from scipy import linalg, sparse |
Creating Matrices
| >>> A : np.matrix(np.random.random((2,2))) |
| >>> B : np.asmatrix(b) |
| >>> C : np.mat(np.random.random((10,5))) |
| >>> D : np.mat([[3,4], [5,6]]) |
Basic Matrix Routines
Inverse
| >>> A.I | Inverse |
| >>> linalg.inv(A) | Inverse |
Transposition
| >>> A.T | Tranpose matrix |
| >>> A.H | Conjugate transposition |
Trace
| >>> np.trace(A) | Trace |
Norm
| >>> linalg.norm(A) | Frobenius norm |
| >>> linalg.norm(A,1) | L1 norm (max column sum) |
| >>> linalg.norm(A,np.inf) | L inf norm (max row sum) |
Rank
| >>> np.linalg.matrix_rank(C) | Matrix rank |
Determinant
| >>> linalg.det(A) | Determinant |
Solving linear problems
| >>> linalg.solve(A,b) | Solver for dense matrices |
| >>> E : np.mat(a).T | Solver for dense matrices |
| >>> linalg.lstsq(F,E) | Least-squares solution to linear matrix equation |
Generalized inverse
| >>> linalg.pinv(C) | Compute the pseudo-inverse of a matrix (least-squares solver |
| >>> linalg.pinv2(C) | Compute the pseudo-inverse of a matrix (SVD) |
Creating Sparse Matrices
| >>> F : np.eye(3, k:1) | Create a 2X2 identity matrix |
| >>> G : np.mat(np.identity(2)) | Create a 2x2 identity matrix |
| >>> C[C > 0.5] : 0 |
| >>> H : sparse.csr_matrix(C) | Compressed Sparse Row matrix |
| >>> I : sparse.csc_matrix(D) | Compressed Sparse Column matrix |
| >>> J : sparse.dok_matrix(A) | Dictionary Of Keys matrix |
| >>> E.todense() | Sparse matrix to full matrix |
| >>> sparse.isspmatrix_csc(A) | Identify sparse matrix |
Sparse Matrix Routines
Inverse
| >>> sparse.linalg.inv(I) | Inverse |
Norm
| >>> sparse.linalg.norm(I) | Norm |
Solving linear problems
| >>> sparse.linalg.spsolve(H,I) | Solver for sparse matrices |
Sparse Matrix Functions
| >>> la, v : sparse.linalg.eigs(F,1) | Eigenvalues and eigenvectors |
| >>> sparse.linalg.svds(H, 2) | SVD |
| >>> sparse.linalg.expm(I) | Sparse matrix exponential |
Matrix Functions
Addition
| >>> np.add(A,D) | Addition |
Subtraction
| >>> np.subtract(A,D) | Subtraction |
Division
| >>> np.divide(A,D) | Division |
Multiplication
| >>> A @ D | Multiplication operator (Python 3) |
| >>> np.multiply(D,A) | Multiplication |
| >>> np.dot(A,D) | Dot product |
| >>> np.vdot(A,D) | Vector dot product |
| >>> np.inner(A,D) | Inner product |
| >>> np.outer(A,D) | Outer product |
| >>> np.tensordot(A,D) | Tensor dot product |
| >>> np.kron(A,D) | Kronecker product |
Exponential Functions
| >>> linalg.expm(A) | Matrix exponential |
| >>> linalg.expm2(A) | Matrix exponential (Taylor Series) |
| >>> linalg.expm3(D) | Matrix exponential (eigenvalue decomposition) |
Logarithm Function
| >>> linalg.logm(A) | Matrix logarithm |
Trigonometric Functions
| >>> linalg.sinm(D) | Matrix sine |
| >>> linalg.cosm(D) | Matrix cosine |
| >>> linalg.tanm(A) | Matrix tangent |
Hyperbolic Trigonometric Functions
| >>> linalg.sinhm(D) | Hypberbolic matrix sine |
| >>> linalg.coshm(D) | Hyperbolic matrix cosine |
| >>> linalg.tanhm(A) | Hyperbolic matrix tangent |
Matrix Sign Function
| >>> np.signm(A) | Matrix sign function |
Matrix Square Root
| >>> linalg.sqrtm(A) | Matrix square root |
Arbitrary Functions
| >>> linalg.funm(A, lambda x: x*x) | Evaluate matrix function |
Decompositions
Eigenvalues and Eigenvectors
| >>> la, v : linalg.eig(A) | Solve ordinary or generalized eigenvalue problem for square matrix |
| >>> l1, l2 : la | Unpack eigenvalues |
| >>> v[:,0] | First eigenvector |
| >>> v[:,1] | Second eigenvector |
| >>> linalg.eigvals(A) | Unpack eigenvalues |
Singular Value Decomposition
LU Decomposition
| >>> U,s,Vh : linalg.svd(B) | Singular Value Decomposition (SVD) |
| >>> M,N : B.shape |
| >>> Sig : linalg.diagsvd(s,M,N) | Construct sigma matrix in SVD |
| >>> P,L,U : linalg.lu(C) | LU Decomposition |
Sparse Matrix Decompositions
>>> np.info(np.matrix)
#python #scipy #data-science #machine-learning