Basics Of Deep Learning

TL;DR:_ Have you even wondered what is so special about convolution? In this post, I derive the convolution from first principles and show that it naturally emerges from translational symmetry._

La connoissance de certains principes supplée facilement à la connoissance de certains faits. (Claude Adrien Helvétius)

During my undergraduate studies, which I did in Electrical Engineering at the Technion in Israel, I was always appalled that such an important concept as convolution [1] just landed out of nowhere. This seemingly arbitrary definition disturbed the otherwise beautiful picture of the signal processing world like a grain of sand in one’s eye. How nice would it be to have the convolution emerge from first principles rather than have it postulated! As I will show in this post, such first principles are the notion of translational invariance or symmetry.

Let me start with the formula taught in basic signal processing courses defining the discrete convolution [2] of two n-dimensional vectors x and w:

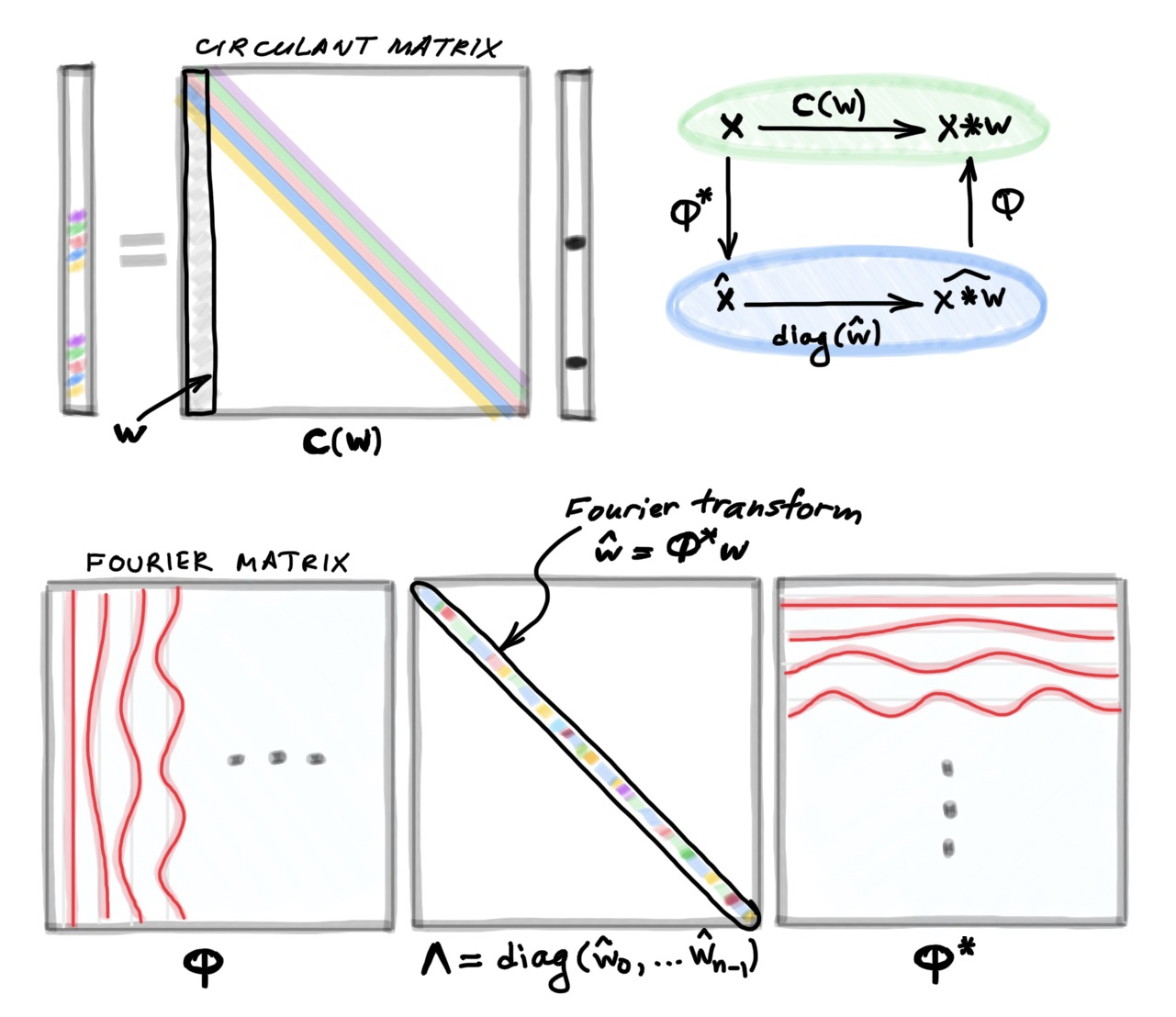
Here, for convenience, I assume that all the indices run from zero to _n_−1 and are modulo n; it is convenient to think of vectors as defined on a circle. Writing the above formula as a matrix-vector multiplication leads to a very special matrix that is called circulant:

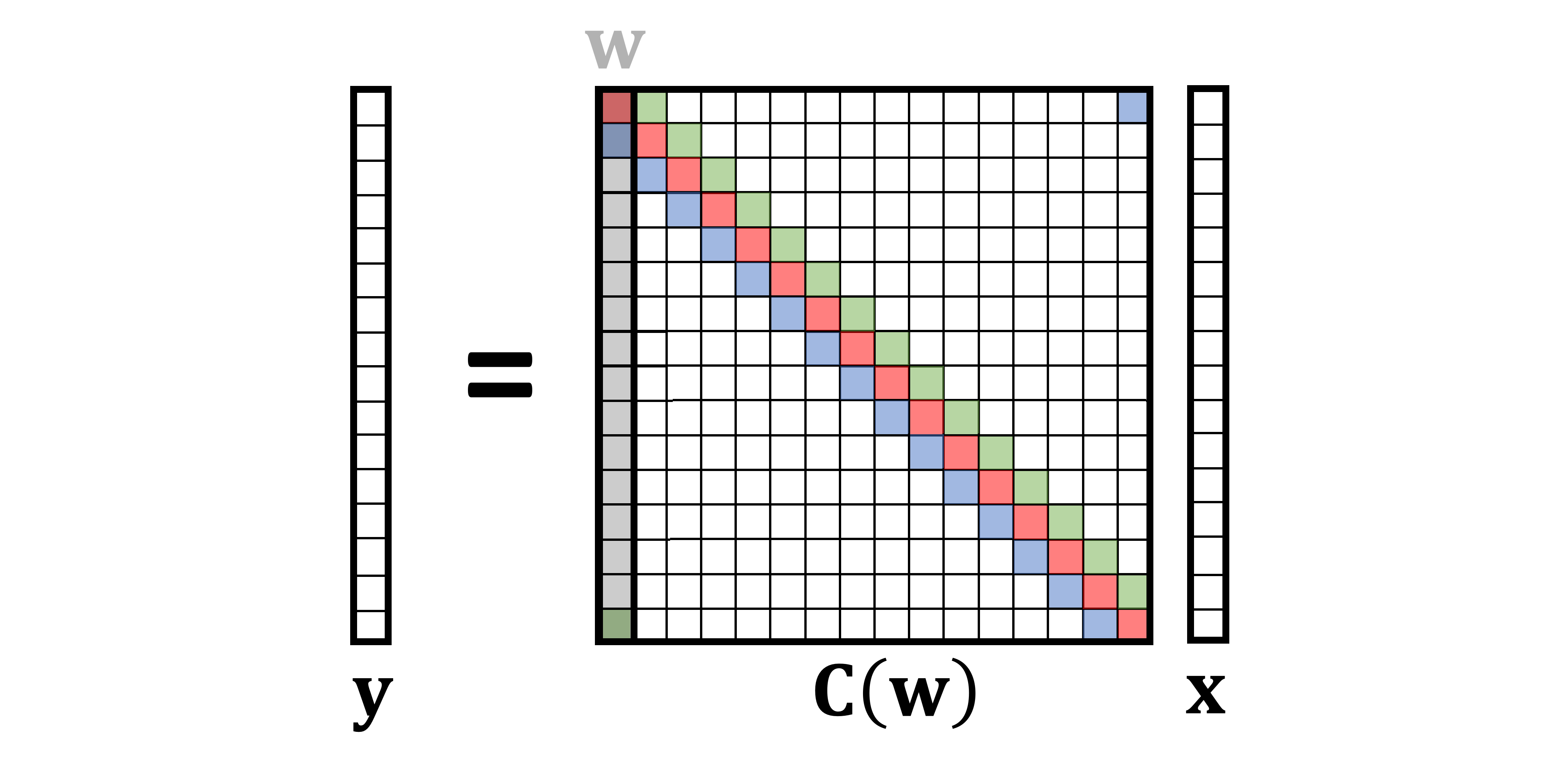
A circulant matrix has multi-diagonal structure, with elements on each diagonal having the same value. It can be formed by stacking together shifted (modulo n) versions of a vector w [3]; for this reason, I use the notation C(w) referring to a circulant matrix formed by the vector w. Since any convolution x∗wcan beequivalently represented as a multiplication by the circulant matrix C(w)x, I will use the two terms interchangeably.

#ai & machine learning #convolution #convolutional newral net #deep learning #deep learning