In this article, we’ll briefly discuss and implement a technique that, in the grand scheme of things, might be getting less attention than it deserves. The previous statement comes from the observation that it’s a well-known issue that some models have a tendency to underperform in production compared to the performance in the model building stage. While there is an abundance of potential culprits for this issue, a common cause could lie in the model selection process.
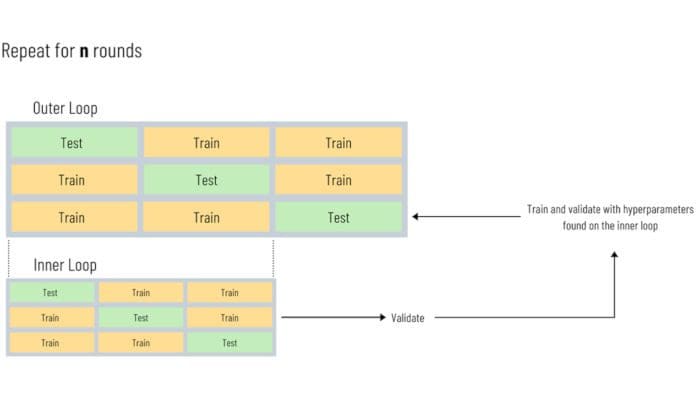
A standard model selection process will usually include a hyperparameter optimization phase, in which, through the use of a validation technique, such as k-fold cross-validation (CV), an “optimal” model will be selected based on the results of a validation test. However, this process is vulnerable to a form of selection bias, which makes it unreliable in many applications. This is discussed in detail on a paper from Gavin Cawley & Nicola Talbot, in which we can find the following nugget of information:
“In a biased evaluation protocol, occasionally observed in machine learning studies, an initial model selection step is performed using all of the available data, often interactively as part of a “preliminary study.” The data are then repeatedly re-partitioned to form one or more pairs of random, disjoint design and test sets. These are then used for performance evaluation using the same fixed set of hyper-parameter values. This practice may seem at first glance to be fairly innocuous, however the test data are no longer statistically pure, as they have been “seen” by the models in tuning the hyperparameters.”
- On Over-fitting in Model Selection and Subsequent Selection Bias in Performance Evaluation, 2010.
To illustrate why this is happening, let’s use an example. Suppose that we are working on a machine learning task, in which we are selecting a model based on n rounds of hyperparameter optimization, and we do this by using a grid search and cross-validation. Now, if we are using the same train and test data at each one of the nth iterations, this means that information of performance on the test set is being incorporated into the training data via the choice of hyperparameters. At each iteration, this information can be capitalized by the process to find the best performing hyperparameters, and that leads to a test dataset that is no longer pure for performance evaluation. If n is large at some point, then we might consider the test set as a secondary training set (loosely speaking).
#overviews #cross-validation #machine learning #python