Vector Calculus

In vector calculus one of the major topics is the introduction of vectors and the 3-dimensional space as an extension of the 2-dimensional space often studied in the cartesian coordinate system. Vectors have two main properties: _direction _and magnitude. In 2-dimensions we can visualize a vector extending from the origin as an arrow (exhibiting both direction and magnitude).

2d vector plot from matplotlib

Intuitively, this can be extended to 3-dimensions where we can visualize an arrow floating in space (again, exhibiting both direction and magnitude).

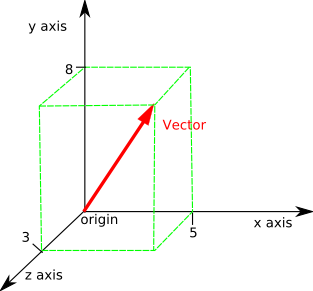
3d vector graph from JCCC

Less intuitively, the notion of a vector can be extended to any number of dimensions, where comprehension and analysis can only be accomplished algebraically. It’s important to note that in any case, a vector does not have a specific location. This means if two vectors have the same direction and magnitude they are the same vector. Now that we have a basic understanding of vectors let’s talk about the gradient vector.

The Gradient Vector

Regardless of dimensionality, the gradient vector is a vector containing all first-order partial derivatives of a function.

Let’s compute the _gradient _for the following function…

The function we are computing the gradient vector for

The gradient is denoted as ∇…

The gradient vector for function f

After partially differentiating…

The gradient vector for function f after substituting the partial derivatives

That is the gradient vector for the function f(x, y). That’s all great, but what’s the point? What can the gradient vector do — what does it even mean?

Gradient Ascent: Maximization

The gradient for any function points in the direction of greatest increase. This is incredible. Imagine you have a function modeling profit for your company. Obviously, your goal is to maximize profit. One way to do this is to compute the gradient vector and pick some random inputs — you can now iteratively update your inputs by computing the gradient and adding those values to your previous inputs until a maximum is reached.

#math #mathematics #artificial-intelligence #optimization #deep learning