Weight and bias are the adjustable parameters of a neural network, and during the training phase, they are changed using the gradient descent algorithm to minimize the cost function of the network. However, they must be initialized before one can start training the network, and this initialization step has an important effect on the network training. In this article, I will first explain the importance of the wight initialization and then discuss the different methods that can be used for this purpose.

Notation

Currently Medium supports superscripts only for numbers, and it has no support for subscripts. So to write the name of the variables, I use this notation: Every character after ^ is a superscript character and every character after _ (and before ^ if its present) is a subscript character. For example

is written as w_ij^[l] in this notation.

Feedforward neural networks

Before we discuss the weight initialization methods, we briefly review the equations that govern the feedforward neural networks. For a detailed discussion of these equations, you can refer to reference [1]. Suppose that you have a feedforward neural network as shown in Figure 1. Here

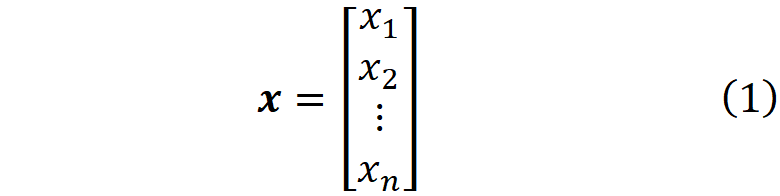
is the network’s input vector. Each x_i is an input feature. The network has L layers and the number of neurons in layer l is n^[l]. The input layer is considered as layer zero. So the number of input features is n^[0]. The output or activation of neuron i in layer l is a_i^[l].

Figure 1 (Image by Author)

The wights for the neuron i in layer _l _can be represented by the vector

where w_ij^[l] represents the weight for the input j (coming from neuron j in layer l-1) going into neuron i in layer l (Figure 2).

Figure 2 (Image by Author)

In layer l, each neuron receives the output of all the neurons in the previous layer multiplied by its weights, w_i1, w_i2, . . . , w_in. The weighted inputs are summed together, and a constant value called bias (b_i^[l]) is added to them to produce the net input of the neuron

The net input of neurons in layer l can be represented by the vector

Similarly, the activation of neurons in layer l can be represented by the activation vector

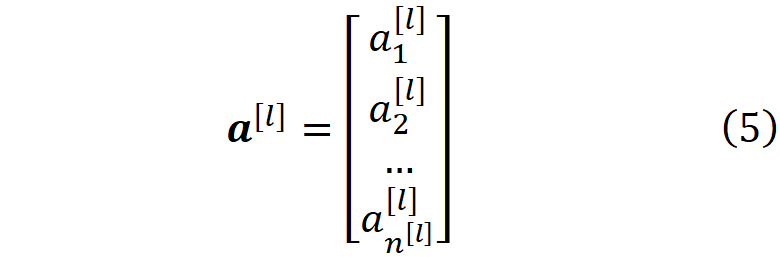
So Eq. 3 can be written as

where the summation has been replaced by the inner product of the weight and activation vectors. The net input is then passed through the activation function g to produce the output or activation of neuron i

We usually assume that the input layer is the layer zero and

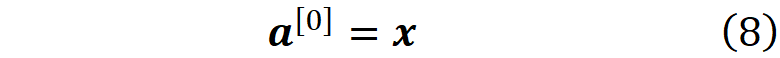
So for the first layer, Eq. 7 is written as

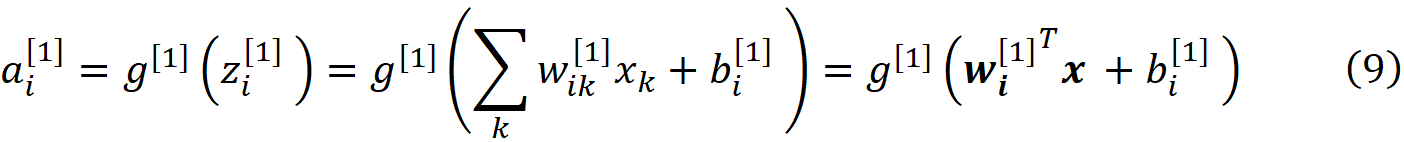
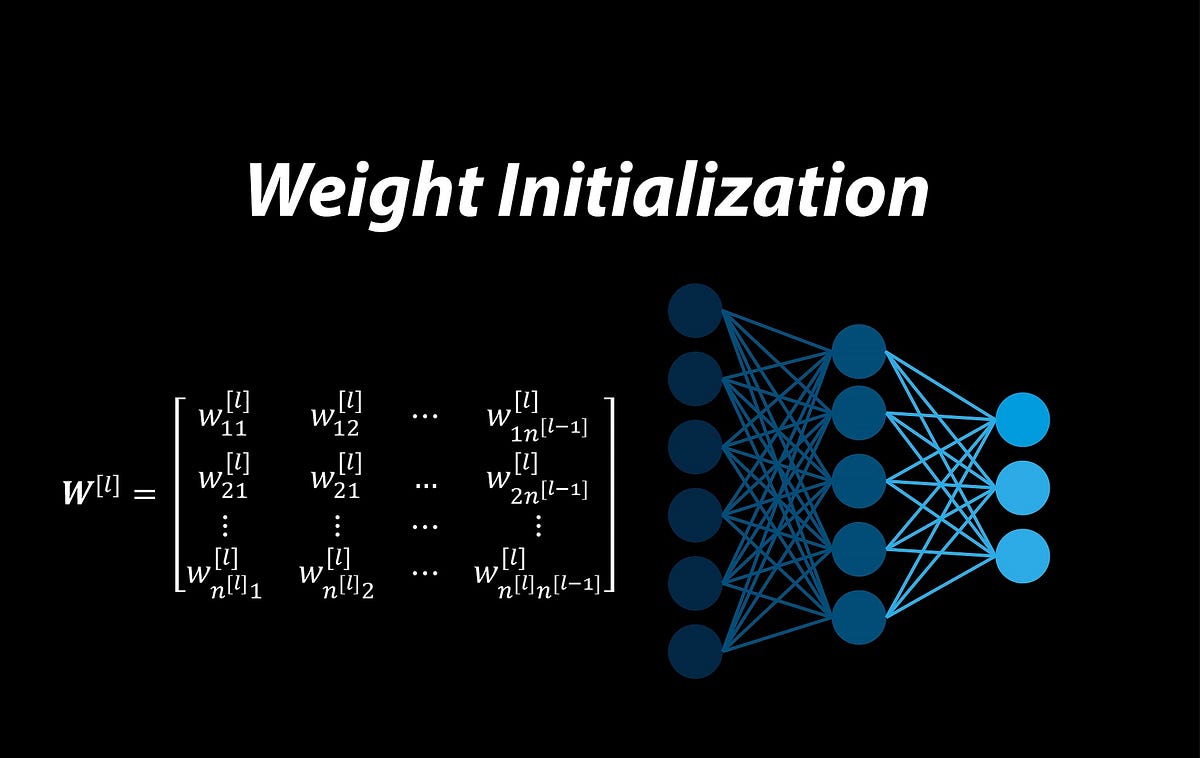
We can combine all the weights of a layer into a weight matrix for that layer

So W^[l] is an n^[l] × n^[l-1] matrix, and the (i,j) element of this matrix gives the weight of the connection that goes from the neuron j in layer l-1 to the neuron i in layer l. We can also have a bias vector for each layer

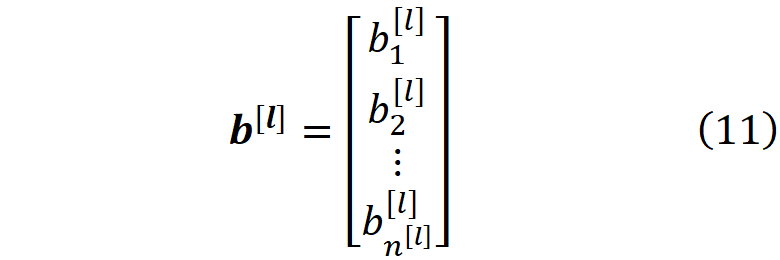
#neural-networks #weight-initialization #deep-learning #machine-learning