You can find the complete code for this tutorial on GitHub here.

We will review the theory for line search methods in optimization, and end with a practical implementation.

Motivation

In all optimization problems, we are ultimately interested in using a computer to find the parameters x that minimize some function f(x) (or -f(x) , if it is a maximization problem). Starting from an initial starting guess x_0, it is common to proceed in one of three ways:

• **Gradient-free optimization **— don’t laugh! Everyone does this. Here we are just guessing the next parameters:

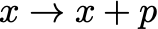
for some random guess p to try to minimize the function, and evaluate the function f(x+p) at the new point to check if the step should be accepted. Actually we all do this — in almost any optimization algorithm, some hyperparameters need to be tuned (e.g. learning rates in machine learning, or initialization of parameters in any optimization problem). While some automatic strategies for tuning these also exist, it’s common to just try different values and see what works best.

• First order methods — these are methods that use the first derivative \nabla f(x) to evaluate the search direction. A common update rule is gradient descent:

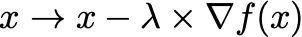
for a hyperparameter \lambda .

• **Second order methods — **here we are using the Hessian \nabla^2 f(x) to pick the next step. A common update rule is Newton’s rule:

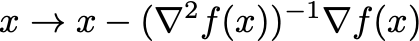
Often, a step size \eta \in (0,1] is included, which is sometimes known as the damped or relaxed Newton’s method.

This, however, is often not sufficient. First, the Hessian is usually expensive to compute. Second, we are generally interested in finding a_ descent direction, _i.e. one for which the product

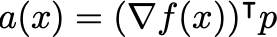
is negative. This is equivalent to requiring that \nabla^2 f(x) is positive definite. To ensure that we are always following a descent direction, q_uasi-Newton methods_ replace the true inverse Hessian with a positive definite estimate, e.g. by regularizing it with a small diagonal matrix:

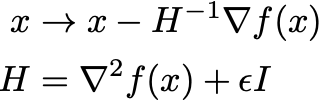
for a small \eps and I as the identity matrix. Note that we _always _choose \eps = 0 if the true Hessian \nabla^2 f(x) is positive definite. Additionally, it is popular to construct an estimate from changing first order gradients that is also cheaper to compute, e.g. using the BFGS algorithm.

#python #programming #machine-learning #algorithms #optimization