In this article we will see how to classify time series data, in particular, how to define and train a 1D convolutional neural network(CNN) on this kind of data and will see different hyper parameter tuning to increase the accuracy.
Introduction
A large amount of data is stored in the form of time series: stock indices, climate measurements, medical tests, etc. Time series classification has a wide range of applications one of them is automated detection of heart and brain diseases.
Classical approaches to the problem involve hand crafting features from the time series data based on fixed-sized windows and training machine learning models, such as ensembles of decision trees. The difficulty is that this feature engineering requires deep expertise in the field.
Recently, deep learning methods such as recurrent neural networks and one-dimensional convolutional neural networks, or CNNs, have been shown to provide state-of-the-art results on challenging activity recognition tasks with little or no data feature engineering, instead using feature learning on raw data.
1-D Convolution for Time Series
Imagine a time series of length n and width k. The length is the number of timesteps, and the width is the number of variables in a multivariate time series. For example, for electroencephalography it is the number of channels (nodes on the head of a person).
The convolution kernels always have the same width as the time series, while their length can be varied. This way, the kernel moves in one direction from the beginning of a time series towards its end, performing convolution. It does not move to the left or to the right as it does when the usual 2-D convolution is applied to images.
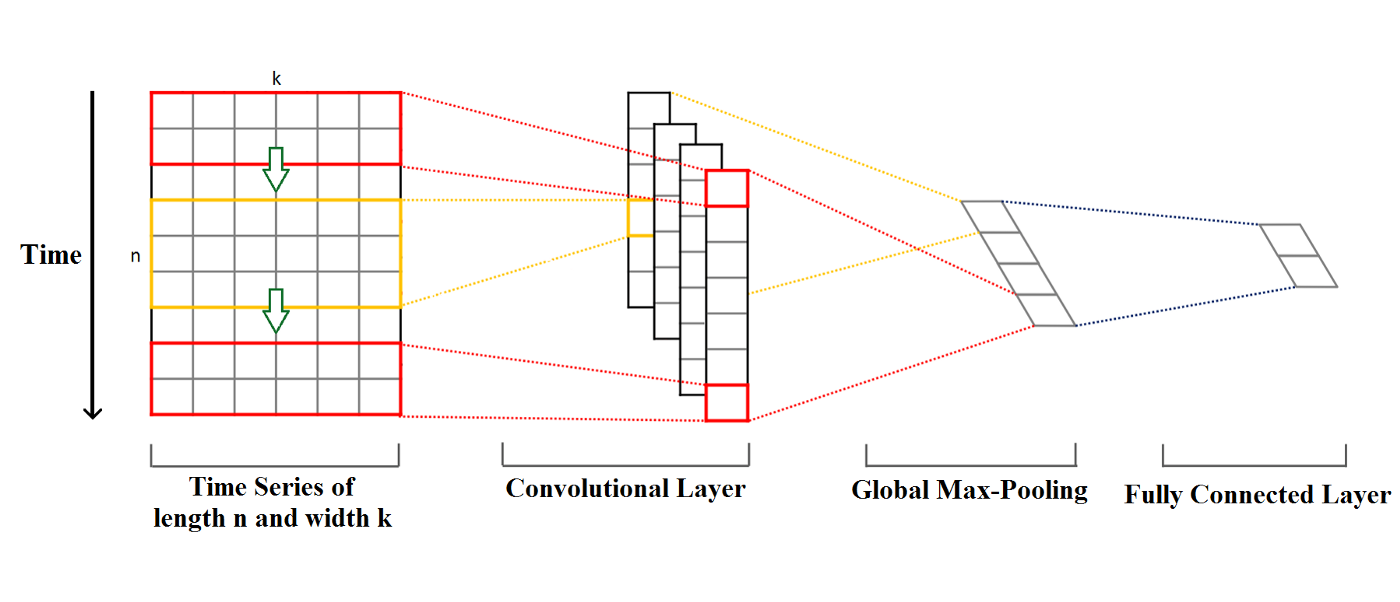
1-D Convolution for Time Series.
The elements of the kernel get multiplied by the corresponding elements of the time series that they cover at a given point. Then the results of the multiplication are added together and a nonlinear activation function is applied to the value. The resulting value becomes an element of a new “filtered” univariate time series, and then the kernel moves forward along the time series to produce the next value. The number of new “filtered” time series is the same as the number of convolution kernels. Depending on the length of the kernel, different aspects, properties, features of the initial time series get captured in each of the new filtered series.
The next step is to apply max-pooling to each of the filtered time series vectors: the largest value is taken from each vector. A new vector is formed from these values, and this vector of maximums is the final feature vector that can be used as an input to a regular fully connected layer. This whole process is illustrated in the picture above.
Let’s start by taking a real life example and build a 1D CNN model.
Here we are working on an emotion recognition/classification of a time series data using a CNN model.
The dataset can be found here.
In this dataset we are trying to predict 3 labels.
- Positive
- Negative
- Neutral
It is a 3 class problem. We can use the same steps for binary classification also.
#timeseries #convolutional-network #deep-learning #neural-networks #machine-learning
