Data scientists are basically modern statisticians. Below are 3 general types of statistics questions that you’ll most likely come across in a data science interview. The reason that these come up so frequently is that they serve as the fundamental building blocks for many data science applications, like Bayesian Machine Learning or Hypothesis Testing.

Keep in mind that there are many many many statistical concepts that are important — for example, I didn’t include Central Limit Theorem but that is still an important concept to know when talking about probability distributions, so take what you’d like out of this.

With that said, here we go!

1. Bayes Theorem / Conditional Probability

Plain and simple, you need to understand Bayes Theorem and conditional probability (see below for equations). One of the most popular machine learning algorithms, Naive Bayes, is built on these two concepts. Additionally, if you enter the realm of **online **machine learning, you’ll most likely be using Bayesian methods.

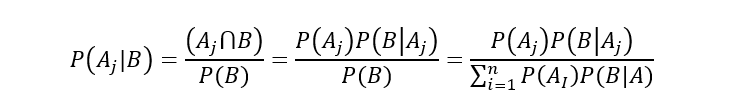
Bayes Theorem

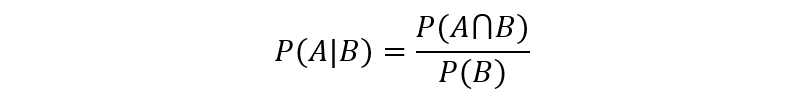
Conditional Probability

Example Question: You’re about to get on a plane to Seattle. You want to know if you should bring an umbrella. You call 3 random friends of yours who live there and ask each independently if it’s raining. Each of your friends has a 2/3 chance of telling you the truth and a 1/3 chance of messing with you by lying. All 3 friends tell you that “Yes” it is raining. What is the probability that it’s actually raining in Seattle?

Answer: You can tell that this question is related to Bayesian theory because of the last statement which essentially follows the structure, “What is the probability A is true given B is true?” Therefore we need to know the probability of it raining in London on a given day. Let’s assume it’s 25%.

P(A) = probability of it raining = 25%

P(B) = probability of all 3 friends say that it’s raining

P(A|B) probability that it’s raining given they’re telling that it is raining

P(B|A) probability that all 3 friends say that it’s raining given it’s raining = (2/3)³ = 8/27

Step 1: Solve for P(B)

P(A|B) = P(B|A) * P(A) / P(B), can be rewritten as

P(B) = P(B|A) * P(A) + P(B|not A) * P(not A)

P(B) = (2/3)³ * 0.25 + (1/3)³ * 0.75 = 0.258/27 + 0.751/27

Step 2: Solve for P(A|B)

P(A|B) = 0.25 * (8/27) / ( 0.258/27 + 0.751/27)

P(A|B) = 8 / (8 + 3) = 8/11

Therefore, if all three friends say that it’s raining, then there’s an 8/11 chance that it’s actually raining.

#data-science #statistics #education #work