This is the first story in the Learn AI Todayseries I’m creating! These stories, or at least the first few, are based on a series of Jupyter notebooks I’ve created while studying/learning **PyTorch **and Deep Learning. I hope you find them as useful as I did!

What you will learn in this story:

• How to Create a PyTorch ModelHow to Train Your ModelVisualize the Training Progress DynamicallyHow the Learning Rate Affects the Training

1. Linear Regression in PyTorch

Linear regression is a problem that you are probably familiar with. In it’s most basic form is no more than fitting a line to a set of points.

1. 1 Introducing the Concepts

Consider the mathematical expression of a line:

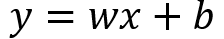
w and bare the two **parameters **or **weights **of this linear model. In machine learning, it is common to use w referring to weights and b referring to the bias parameter.In machine learning when we are training a model we are basically finding the optimal parameters w and b for a given set of input/target (x,y) pairs. After the model is trained we can compute the model estimates. The expression will now look

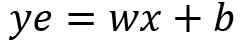
where I change the name o y to ye (y estimate) because the solution will not be exact.The Mean Square Error (MSE) is simply mean((ye-y)²) — the mean of the squared deviations between targets and estimates. For a regression problem, you can indeed minimize the MSE in order to find the best w and b .The idea of linear regression can be generalized using algebra matrix notation to allow for multiple inputs and targets. If you want to learn more about the mathematical exact solution for the regression problem you can search about Normal Equation.

1.2 Defining the Model

PyTorch nn.Linear class is all that you need to define a linear model with any number of inputs and outputs. For our basic example of fitting a line to a set of points consider the following model:

Note:_ I’m using _Module _from fastai library as it makes the code cleaner. If you want to use pure PyTorch you should use nn.Module instead and you need to add super().__init__() in the __init__ method. fastai Module does that for you._If you are familiar with Python classes, the code is self-explanatory. If not, consider doing some study before diving into PyTorch. There are many online tutorials and lessons covering the topic.Back to the code. In the __init__ method, you define the layers of the model. In this case, it is just one linear layer. Then, the forward method is the one that is called when you call the model. Similar to __call__ method in normal Python classes.Now you can define an instance of your LinearRegression model as model = LinearRegression(1, 1) indicating the number of inputs and outputs.Maybe you are now asking why I don’t simply do model = nn.Linear(1, 1) and you are absolutely right. The reason I’m having all the trouble of defining LinearRegression class is just to work as a template for future improvements as you will find later.

1.3 How to Train Your Model

The training process is based on a sequence of 4 steps that repeat iteratively:

• **Forward pass: **The input data is given to the model and the model outputs are obtained — outputs = model(inputs)**The loss function is computed: **For the purpose of the linear regression problem, the loss function we are using is the mean squared error (MSE). We often refer to this function as the criterion — loss = criterion(outputs, targets)Backward pass: The gradients of the loss function with respect to each learnable parameter are computed. Remember that we want to reduce the loss function to make the outputs close to the targets. The gradients tell how the loss change if you increase or decrease each parameter — loss.backwards()**Update parameters: **Update the value of the parameters by a small amount in the direction that reduces the loss. The method to update the parameters can be as simple as subtracting the value of the gradient multiplied by a small number. This number is referred to as the **learning rate **and the optimizer I just described is the Stochastic Gradient Descent (SGD) — optimizer.step()

I didn’t define exactly the criterion and optimizer yet but I will in a minute. This is just to give you a general overview and understanding of the steps for a training iteration or as usually called — a training epoch.Let’s define our fit function that will do all the required steps.

#data-science #artificial-intelligence #deep-learning #learn-ai-today #deep learning