Binary Search in Java – Explained with Code Examples

Learn how the binary search algorithm works with code examples. Learn how to implement the algorithm in Java. The differences between binary search algorithm and binary search tree.

Algorithms provide step by step instructions on solving specific problems. They help you solve problems using efficient, standard, and reusable steps.

The binary search algorithm is one of the commonly used algorithms in programming. It is used to search and find an element in a sorted array.

The binary search algorithm is different from the binary search tree. We'll talk about their differences later in this article.

How Does the Binary Search Algorithm Work?

In this section, you'll see a practical application of binary search using diagrams.

The binary search algorithm is a divide and conquer algorithm that searches for a specific element in a sorted array.

Note that the collection of elements/array must be sorted for the algorithm to work efficiently.

Here are the steps involved with the binary search algorithm:

Step #1 - Sort the Array

In order to start the search, you'll need to have a sorted array. The image above has a collection of numbers sorted in ascending order: 2,3,6,8,9,13,20.

Let's assume that the element we're looking for is 13. We'll store this in a variable called number_to_search_for.

Step #2 - Choose Low and High Values

sorted array with low and high pointers

The first index of the array will be denoted as low while the highest index will be denoted as high.

These values will help you get the midpoint of the array.

Midpoint = (low + high) / 2.

Step #3 - Choose Midpoint/Middle Element

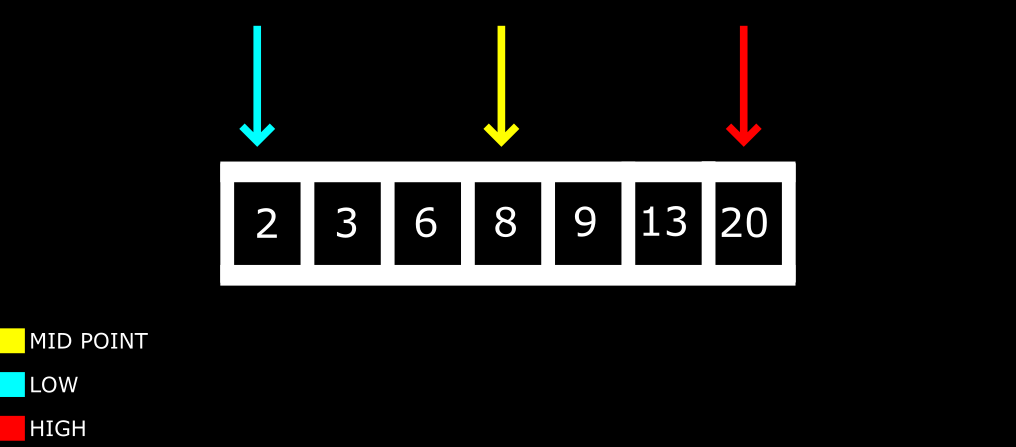
sorted array with low, high, and middle pointers

The image above shows the midpoint which is at the center of the array.

Now that you know the low, high, and midpoint of the array, the binary search operation can begin.

Step #4 - Binary Search

This is what happens during the binary search:

1. If number_to_search_for  is equal to midpoint, the midpoint index will be returned.
2. If number_to_search_for is greater than midpoint, search through the elements on the right side of the midpoint.
3. If number_to_search_for is less than midpoint, search through the elements on the left side  midpoint.

Step 3 will only be relevant if step 2 is false. If  number_to_search_for doesn't exist in the array, return -1.

Let's simplify the steps above using diagrams:

This is the array we're working with: 2,3,6,8,9,13,20.

number_to_search_for = 13.

midpoint = 8.

low = 2.

high = 20.

Iteration #1

From the steps listed above, you begin by comparing number_to_search_for to midpoint.

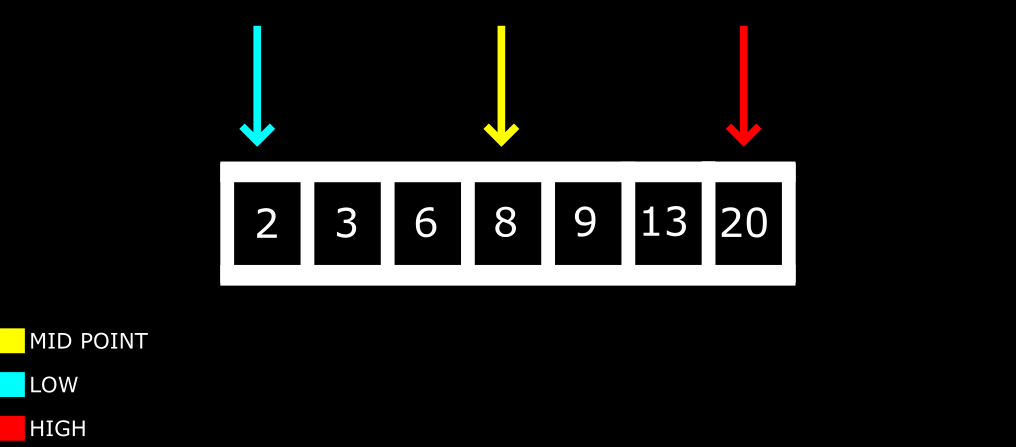
sorted array with low, high, and middle pointers

As you can see in the diagram above, the value of number_to_search_for and midpoint are not the same.

The next step is to find out if the number_to_search_for is greater than or less than midpoint.

In our own case, it is greater than midpoint so we'll focus on the elements on the right side of the midpoint — 9, 13, and 20.

This makes the search much faster because we've cut out half of the array that isn't needed.

We'll repeat all the steps for those elements as well.

The steps will run continuously until the element is found. In a case where the element doesn't exist, -1 will be returned.

Iteration #2

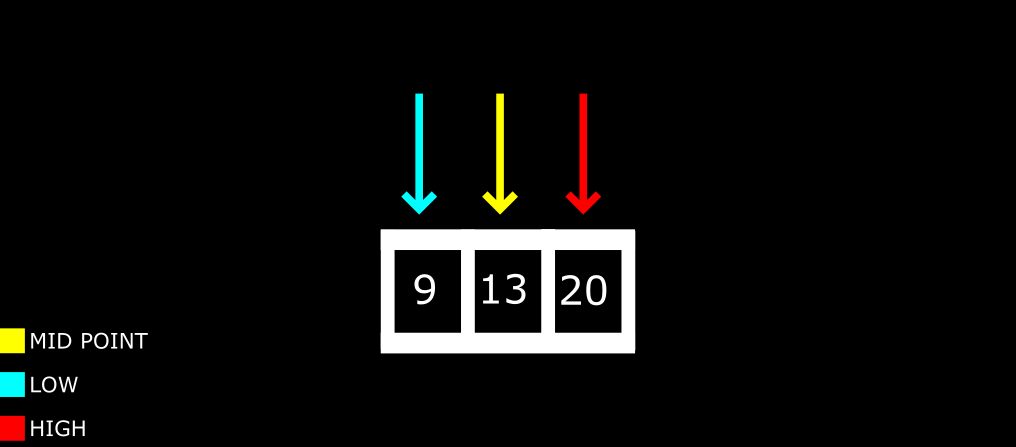
sorted array with low, high, and middle pointers

Comparing the midpoint and number_to_search_for in the diagram above, we have the same value.

At this point, the binary search operation stops because we've found the number. The index of the number will be returned.

That is: index 5 from the original array (2,3,6,8,9,13,20).

In the next section, you'll see how to implement the algorithm in Java.

Binary Search Algorithm Example in Java

class BinarySearch {
    private static int binarySearch(int numArray[], int number_to_search_for) {
        int low = 0;
        int high = numArray.length - 1;
        
        while (low <= high){
            int middleIndex = (low + high) / 2;
            int middleIndexNumber = numArray[middleIndex];
            
            if (number_to_search_for == middleIndexNumber){
                return middleIndex;
            }
            if (number_to_search_for < middleIndexNumber){
                high = middleIndex - 1;
            }
            if (number_to_search_for > middleIndexNumber){
                low = middleIndex + 1;
            }
        }
        
        return -1;
  }
    public static void main(String args[]) {
        
        int[] arrayofnums = {2,3,6,8,9,13,20};
        
        System.out.println(binarySearch(arrayofnums, 13));
        // 5
        
    }

}

In the code above, we created a method called binarySearch with two parameters — int numArray[] and int number_to_search_for:

private static int binarySearch(int numArray[], int number_to_search_for){...}

The first parameter represents the array to be searched through. The second represents the number to be searched for.

Next, we defined the low and high variables to represent the first and last index of the array:

int low = 0;
int high = numArray.length - 1;

After that, we created a while loop with if statements matching the 3 steps used in the previous section (Step #4 - Binary Search section):

while (low <= high){
    int middleIndex = (low + high) / 2;
    int middleIndexNumber = numArray[middleIndex];
           
    if (number_to_search_for == middleIndexNumber){
        return middleIndex;
    }
    if (number_to_search_for < middleIndexNumber){
        high = middleIndex - 1;
    }
    if (number_to_search_for > middleIndexNumber){
        low = middleIndex + 1;
    }
}

You can have a look at the Step #4 - Binary Search section to understand the code in the while loop.

We then returned -1 after the while loop in case the number being searched for doesn't exist in the array.

Lastly, we tested the method to be sure the functionality worked as expected:

public static void main(String args[]) {
        
     int[] arrayofnums = {2,3,6,8,9,13,20};
        
     System.out.println(binarySearch(arrayofnums, 13));
     // 5
        
}

We specified 13 as the second parameter and got index 5 returned.

If you use a number that doesn't exist in the array, you'll get -1 returned.

Differences Between Binary Search Algorithm and Binary Search Tree

Although both binary search algorithm and binary search tree are both used for searching, there are some differences in mode operation of operation and data structure.

Here are some differences:

• Binary search algorithm is used for searching while binary search tree is used for searching, insertion, and deletion.
• Binary search algorithm compares the middle element with the element being searched for while binary search tree compares the value of nodes in a tree.
• Binary search algorithm searches through an array or list while binary search tree traverses through a tree of nodes.

You can read more about the binary search tree here.

Summary

In this article, we talked about the binary search algorithm. It is to search for specific elements in an array.

We saw how the algorithm works using visual guides. Then we saw an implementation of the algorithm in Java.

Lastly, we saw the differences between binary search algorithm and binary search tree.

Happy coding!

Source: https://www.freecodecamp.org

#binarysearch #java #algorithms