Logistic regression is a popular method since the last century. It establishes the relationship between a categorical variable and one or more independent variables. This relationship is used in machine learning to predict the outcome of a categorical variable. It is widely used in many different fields such as the medical field, trading and business, technology, and many more. This article explains the process of developing a binary classification algorithm and implements it on a medical dataset.

Problem Statement

In this article, a logistic regression algorithm will be developed that should predict a categorical variable. Ultimately, it will return a 0 or 1.

Important Equations

The core of the logistic regression is a sigmoid function that returns a value from 0 to 1. Logistic regression uses the sigmoid function to predict the output. Here is the sigmoid activation function:

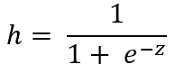
z is the input features multiplied by a randomly initialized term theta.

Here, X is the input features and theta is the randomly initialized values that will be updated in this algorithm. Generally, we add a bias term as well.

Another important term is the cost function. Cost function gives the intuition on how far the original values are from the predicted values. Here is the cost function expression:

Then, we need to update our randomly initialized theta values using the following equation:

Model Development

Step 1: Develop the hypothesis.

The hypothesis is simply the implementation of the sigmoid function.

def hypothesis(X, theta):
    z = np.dot(theta, X.T)
    return 1/(1+np.exp(-(z))) - 0.0000001

I deducted 0.0000001 from the output here because of this expression in the cost function:

If the outcome of the hypothesis expression comes out to be 1, then this expression will turn out to be the log of zero. To mitigate that, I used this very small number at the end.

#towards-data-science #logistic-regression #machine-learning #data-science #python