Bootstrapping Examples: Yield Curve Calculation

Definition of Bootstrapping

The term bootstrapping refers to the technique of carving out a zero-coupon yield curve from the market prices of a set of coupon-paying bonds. Primarily, we use the bootstrapping technique to calculate Treasury bill yields offered by the government, which aren’t always available for every time period.

Examples of Bootstrapping

Some of the examples of bootstrapping are given below:

Example #1

Let us take the example of two 5% coupons paying the bond with zero credit-default risks and a par value of $100 with the clean market prices (exclusive of accrued interest) of $99.50 and $98.30, respectively and having time for the maturity of 6 months and 1 year respectively. First, determine the spot rate for the 6-month and 1-year bonds. Please note that this is a par curve where the coupon rate equals the yield to maturity.

At the end of 6 months, the bond will pay a coupon of $2.5 (= $100 * 5% / 2) plus the principal amount (= $100), which sums up to $102.50. The bond is trading at $99.50. Therefore, we can calculate the 6-month spot rate S0.5y as follows,

$99.50 = $102.50 / (1 + S0.5y/2)

S5y = 6.03%

At the end of another 6 months, the bond will pay another coupon of $2.5 (= $100 * 5% / 2) plus the principal amount (= $100), which sums up to $102.50. The bond is trading at $98.30. Therefore, the 1-year spot rate S1y can be calculated using S0.5y as,

C PROGRAMMING Course Bundle - 8 Courses in 1
29+ Hours of HD Videos | 8 Courses | Verifiable Certificate of Completion | Lifetime Access
4.5

$99.50 = $2.50 / (1 + S0.5y/2) + $102.50 / (1 + S1y/2)2

$99.50 = $2.50 / (1 + 6.03%/2) + $102.50 / (1 + S1y/2)2
S1y = 6.80%

So, as per the market prices, the spot rate for the first 6-month period is 6.03%, and the forward rate for the second 6-month period is 6.80%

Example #2

Let us take another example of some coupon-paying bonds with zero credit-default risks, each with a par value of $100 and trading at par value. However, each has a varying maturity period ranging from 1 year to 5 years. Determine the spot rate for all the bonds. Please note that this is a par curve where the coupon rate equals the yield to maturity. The detail is given in the table below:

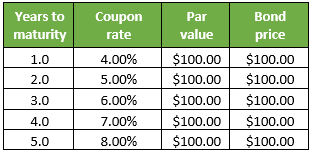
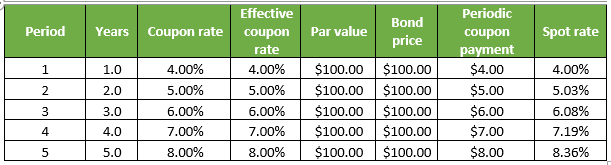
1. At the end of 1 year, the bond will pay a coupon of $4 (= $100 * 4%) plus the principal amount (= $100), which sums up to $104 while the bond is trading at $100. Therefore, the 1-year spot rate S1y can be calculated as,

$100 = $104 / (1 + S1y)

S1y = 4.00%

2. At the end of the 2nd year, the bond will pay a coupon of $5 (= $100 * 5%) plus the principal amount (= $100), which is up to $105 while the bond is trading at $100. Therefore, the 2-year spot rate S2y can be calculated using S1y as,

$100 = $4 / (1 + S1y) + $105 / (1 + S2y)2

$100 = $4 / (1 + 4.00%) + $105 / (1 + S2y)2
S1y = 5.03%

3. At the end of the 3rd year, the bond will pay a coupon of $6 (= $100 * 6%) plus the principal amount (= $100), which is up to $106 while the bond is trading at $100. Therefore, the 3-year spot rate S3y can be calculated using S1y and S2y as,

$100 = $4 / (1 + S1y) + $5 / (1 + S2y)2 + $106 / (1 + S3y)3

$100 = $4 / (1 + 4.00%) + $5 / (1 + 5.03%)2 + $106 / (1 + S3y)3
S3y = 6.08%

4. At the end of the 4th year, the bond will pay a coupon of $7 (= $100 * 7%) plus the principal amount (= $100), which is up to $107 while the bond is trading at $100. Therefore, we can calculate the 4-year spot rate S4y using S1y, S2y, and S3y as follows,

$100 = $4 / (1 + S1y) + $5 / (1 + S2y)2 + $6 / (1 + S3y)3 + $107 / (1 + S4y)4

$100 = $4 / (1 + 4.00%) + $5 / (1 + 5.03%)2 + $6 / (1 + 6.08%)3 + $107 / (1 + S4y)4
S4y = 7.19%

5. At the end of the 5th year, the bond will pay a coupon of $8 (= $100 * 8%) plus the principal amount (= $100), which sums up to $108 while the bond is trading at $100. Therefore, we can calculate the 5-year spot rate S5y using S1y, S2y, S3y, and S4y as follows,

$100 = $4 / (1 + S1y) + $5 / (1 + S2y)2 + $6 / (1 + S3y)3 + $7 / (1 + S4y)4 + $108 / (1 + S5y)5

$100 = $4 / (1 + 4.00%) + $5 / (1 + 5.03%)2 + $6 / (1 + 6.08%)3 + $7 / (1 + 7.19%)4 + $108 / (1 + S5y)5
S5y = 8.36%

Conclusion – Bootstrapping Examples

The bootstrapping technique may be simple, but determining the real yield curve and then smoothening it out can be a tedious and complicated activity involving lengthy mathematics, primarily using bond prices, coupon rates, par value, and the number of compounding per year.