Statistics is the science of learning from data. Statistical knowledge aids in the proper methods for collecting data, using correct methods for analyzing data, and effectively presenting the results derived from data. These methods are crucial to making decisions and predictions, whether it be predicting the consumer demand for a product; using text-mining to filter spam emails; or making real-time decisions in self-driving cars. Most times when conducting research, it is impractical to collect data from the population. This can be because of budget and/or time constraints, among other factors. Instead, a subset of the population is taken, and insight is gathered from that subset to learn more about the population. It means then that suitably accurate information can be obtained quickly and relatively inexpensively from an appropriately drawn sample. However, many things can affect how well a sample reflects the population; and therefore, how valid and reliable the conclusions will be. Because of this, let us talk about bootstrapping statistics.

Image by Trist’n Joseph
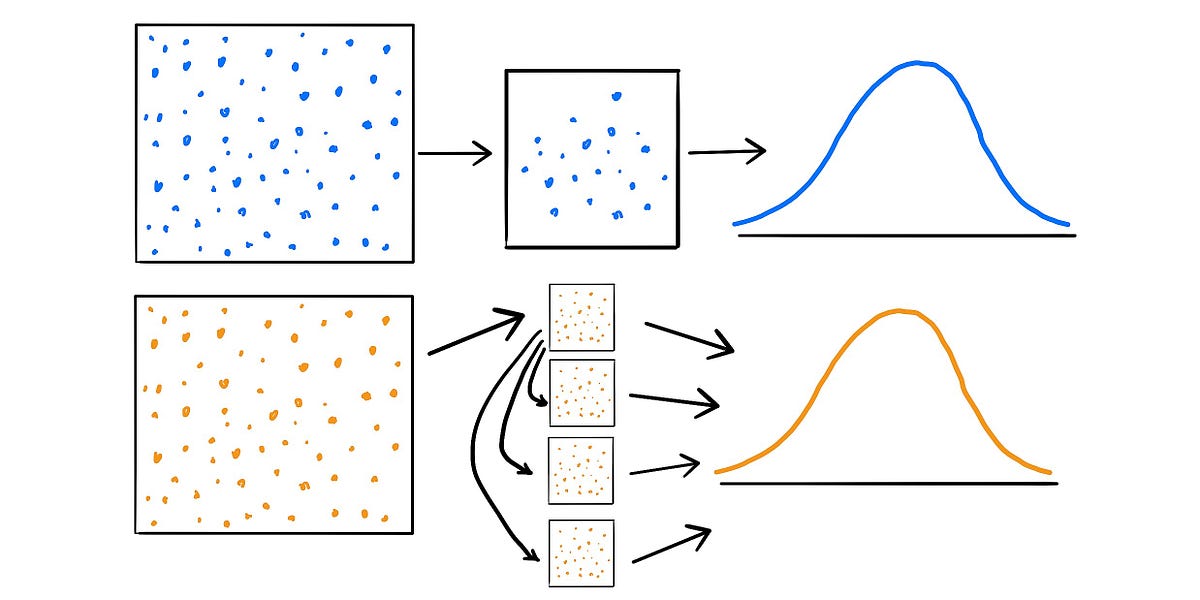
“Bootstrapping is a statistical procedure that resamples a single dataset to create many simulated samples. This process allows for the calculation of standard errors, confidence intervals, and hypothesis testing” (_Forst). _A bootstrapping approach is an extremely useful alternative to the traditional method of hypothesis testing as it is fairly simple and it mitigates some of the pitfalls encountered within the traditional approach, which will be discussed later. Statistical inference generally relies on the sampling distribution and the standard error of the feature of interest. The traditional approach (or large sample approach) draws one sample of size _n _from the population, and that sample is used to calculate population estimates to then make inferences on. Now, in reality, only one sample has been observed. However, there is the idea of a sampling distribution, which is a theoretical set of all possible estimates if the population were to be resampled. The theory states that, under certain conditions such as large sample sizes, the sampling distribution will be approximately normal, and the standard deviation of the distribution will be equal to the standard error. But what happens if the sample size is not sufficiently large? Then, it cannot necessarily be assumed that the theoretical sampling distribution is normal. This then makes it difficult to determine the standard error of the estimate, and harder to draw reasonable conclusions from the data.

Image by Trist’n Joseph
As with the traditional approach, a sample of size _n _is drawn from the population within the bootstrapping approach. Let us call this sample S. Then, rather than using theory to determine all possible estimates, the sampling distribution is created by resampling observations with replacement from S, m times, with each resampled set having n observations. Now, if sampled appropriately, S should be representative of the population. Therefore, by resampling S m times with replacement, it would be as if m samples were drawn from the original population, and the estimates derived would be representative of the theoretical distribution under the traditional approach. It must be noted that increasing the number of resamples, m, will not increase the amount of information in the data. That is, resampling the original set 100,000 times is not more useful than only resampling it 1,000 times. The amount of information within the set is dependent on the sample size, n, which will remain constant throughout each resample. The benefit of more resamples, then, is to derive a better estimate of the sampling distribution.

Image by Trist’n Joseph
Now that we understand the bootstrapping approach, it must be noted that the results derived are basically identical to those of the traditional approach. Additionally, the bootstrapping approach will always work because it does not assume any underlying distribution of the data. This contrasts with the traditional approach which theoretically assumes that the data are normally distributed. Knowing how the bootstrapping approach works, a logical question to arise is “does the bootstrapping approach rely too much on the observed data?” This is a good question, given that the resamples are derived from the initial sample. And because of this, it is logical to assume that an outlier will skew the estimates from the resamples. Although this is true, if the traditional approach is considered, it will be seen that an outlier within the dataset will also skew the mean and inflate the standard error of the estimate. Therefore, while it might be tempting to think that an outlier can show up multiple times within the resampled data and skew the results, thus making the traditional approach better, the bootstrapping approach relies as much on the data as does the traditional approach. “The advantages of bootstrapping are that it is a straightforward way to derive the estimates of standard errors and confidence intervals, and it is convenient since it avoids the cost of repeating the experiment to get other groups of sampled data. Although it is impossible to know the true confidence interval for most problems, bootstrapping is asymptotically consistent and more accurate than using the standard intervals obtained using sample variance and the assumption of normality” (Cline).
#data-science #data #statistics #data analysis