MO’s Algorithm aka Square Root Decomposition, a very efficient and easy technique to solve **Range Query Problems (RQP). **For MO’s Algorithm to work, the RQP has to be offline. In this post, we will understand about RQP, Offline RPQ, Naive Approach to solve RQP and an Efficient Approach using MO’s Algorithm.

What is a Range Query Problem?

You are given a sequence **_A _**of **_N _**values A₁, A₂, A₃, …, Aₙ. You also are given **_Q _**queries. In each query, you will be given two values l and r. Your task is to perform a function **_f(l, r) _**on the elements in the subsequence Aₗ, Aₗ₊₁, …, Aᵣ₋₁, Aᵣ

What is an Offline Query Problem?

An RQP is offline if it satisfies the following conditions

1. All Queries are known beforehand.
2. There are no update operations on the given sequence.

Problem Statement

You are given a sequence **_A _**of **_N _**values **_A₁, A₂, A₃, …, Aₙ. _**You also are given **_Q _**queries. Each query will have two values **_l _**and r. Your task is to find the number of vowels in the range Aₗ, Aₗ₊₁, …, Aᵣ₋₁, Aᵣ

Naive Approach

A Simple approach is to iterate from l to r for each query (l, r) and find the number of vowels in the range. A sample code snippet is given below.

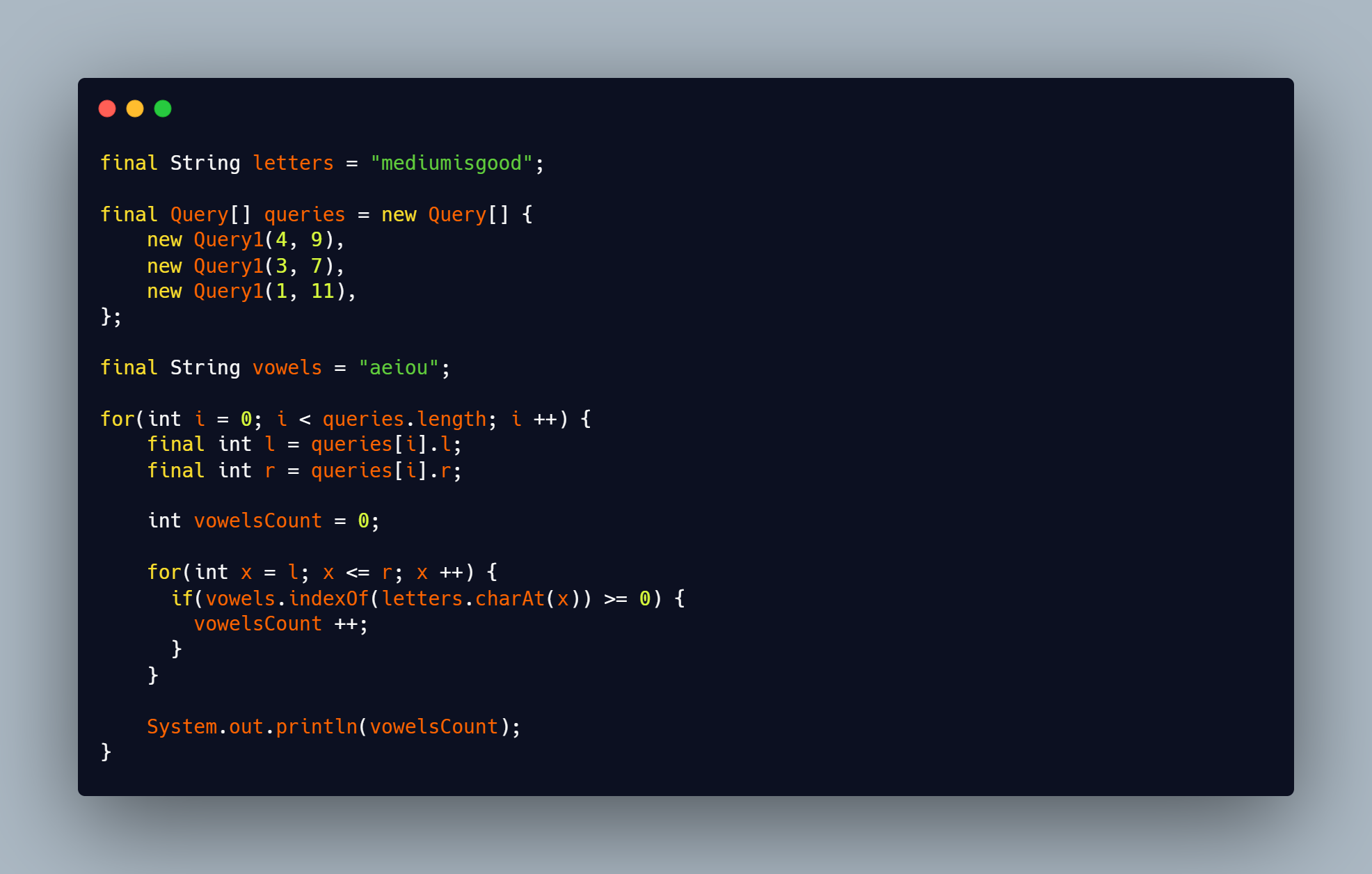
Java Code Snippet for Naive Approach

Time Complexity

The time complexity of the above code would be O(N*Q) where N = Number of elements in the Sequence and Q = Number of Queries.

MO’s Algorithm

MO’s algorithm follows two simple steps to make the solution more efficient

1. Divide the sequence into _√N _blocks.
2. Rearrange all the queries in such a way that a query (l₁, r₁) comes before (l₂, r₂) if

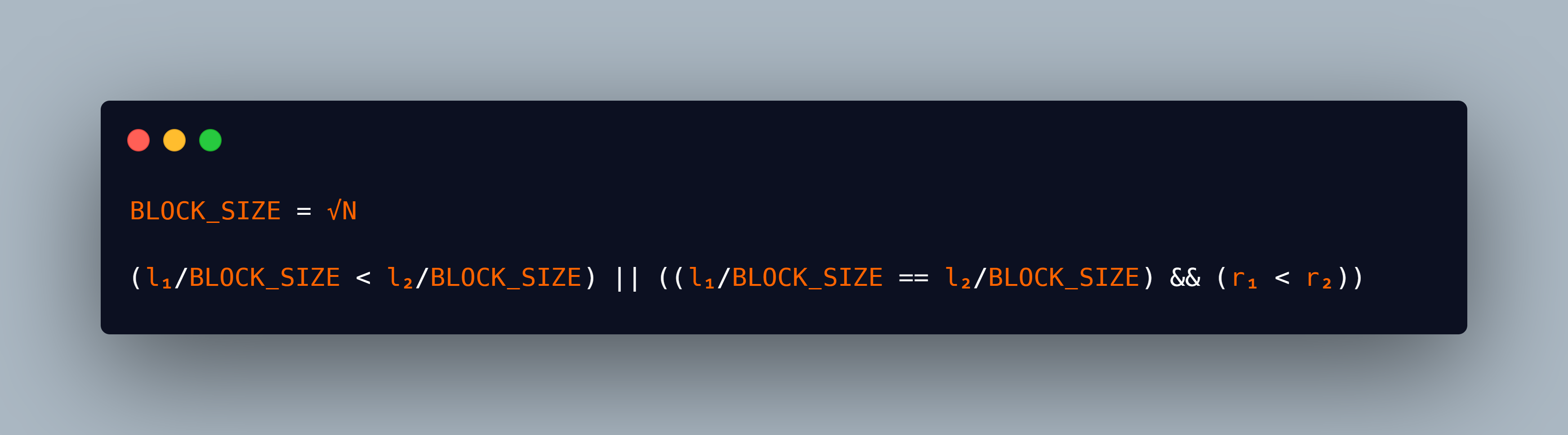
MO’s Order Conditions

By rearranging the queries in the above manner, we tend to process all the queries of one block before processing the queries of another block, thus minimizing the pointer movement of i and **_j. _**Now, we apply MO’s technique in our problem

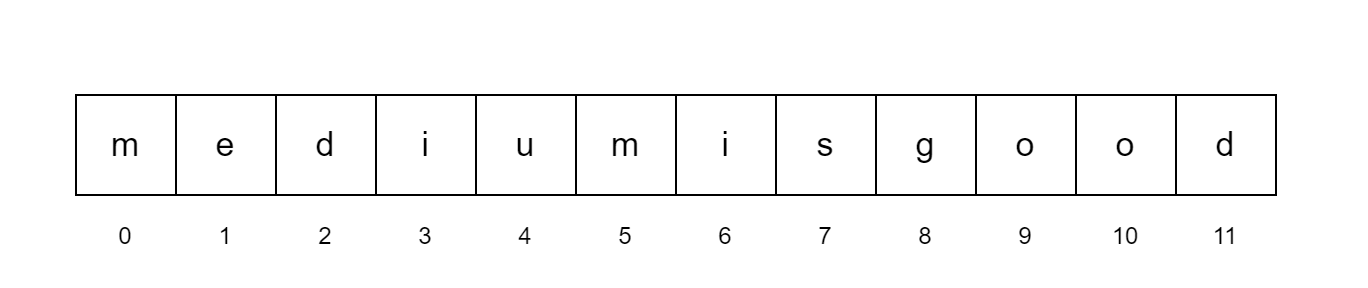
Sample Sequence

Now we have a sequence of letters of size 12. Now we apply the first step, calculate block size in our sequence

**_BLOCK_SIZE = √12 ≈ 3, _**So, we divide our sequence to 3 blocks each of size 4.

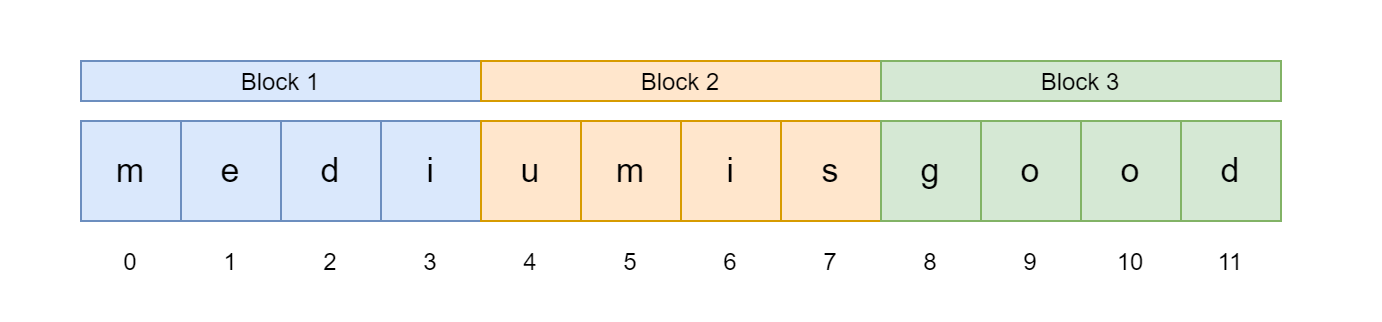
Sequence divided into √N blocks

Now consider that the following queries are given to us (4, 9), (3, 7), (2, 8), (0, 5), (7, 10), (1, 11)

Out next step is to arrange the above queries based on **MO’s order. **The java code snippet for sorting logic is given below

#algorithms #programming #coding #competitive-programming #java #algorithms