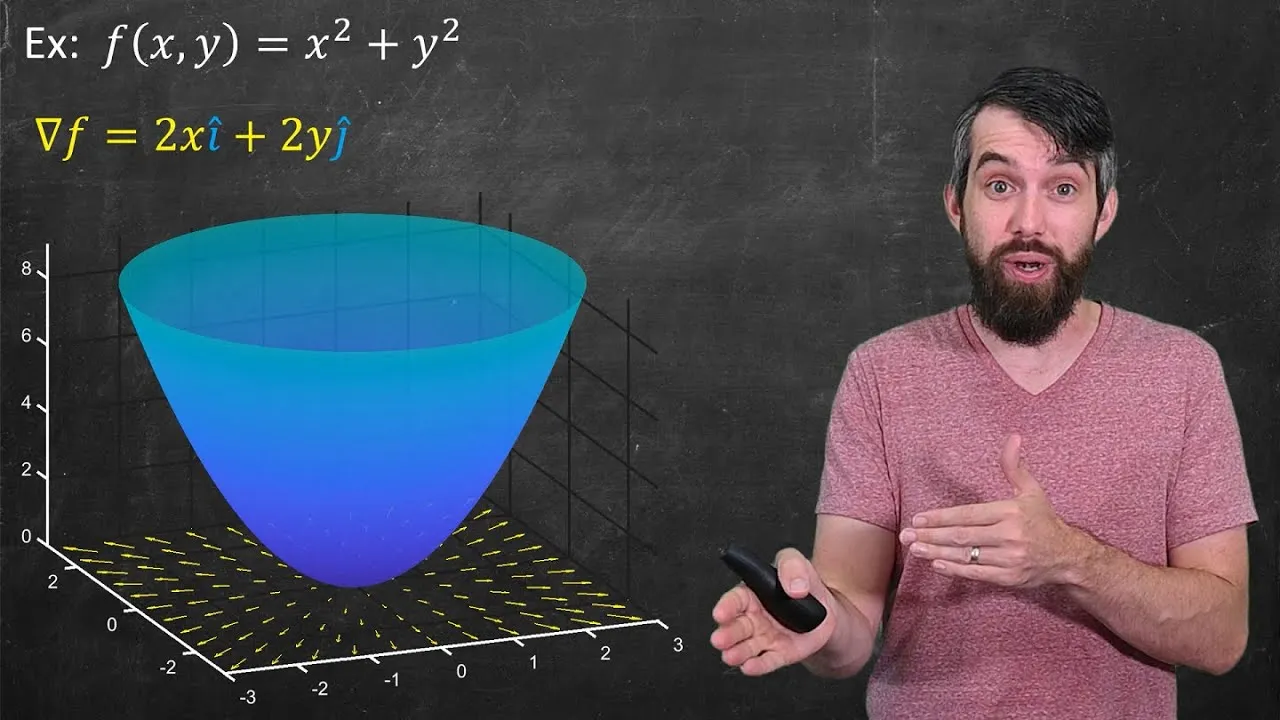
A gradient vector field is a vector field that represents the direction and magnitude of the greatest rate of change of a scalar field. In other words, it points in the direction of the steepest ascent of the scalar field.

One prominent example of a vector field is the Gradient Vector Field. Given any scalar, multivariable function f: R^n\to R, we can get a corresponding vector field that has a precise geometrical meaning: the vectors point in the direction of maximal increase of the function.

Subscribe: https://www.youtube.com/@DrTrefor/featured