In this article, we’ll explore and visualize a classic mathematical model used for modeling the spread of infectious disease: the SIR model.

Population compartments

The model splits the population into three compartments:

• The susceptible (S): Individuals who are yet to contract the disease.
• The** infectious** (I): Individuals who have contracted the disease and are capable of spreading it to susceptible individuals.
• The **recovered **®: Individuals who have recovered from the disease and became immune to it.

The sum of these compartments represents the number of individuals in the population, which is denoted by N:

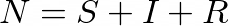
Our goal is to model how these compartments fluctuate over time, and so we’ll consider them to be functions with respect to time:

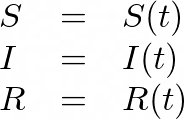
The SIRD model considers another compartment (D) for deceasedindividuals.

Compartment transition

In the SIR model, the transition between compartments takes the following path: susceptible → infectious → recovered. Each transition happens at a different rate.

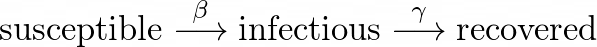
The rate at which susceptible individuals come into contact with infectious individuals, thus contracting the disease, is called the **infectious rate **(β). Once infected, the rate at which they recover is called the **recovery rate **(γ).

The SIRS model takes into account the possibility of recovered individuals becoming susceptible again, due to loss of immunity.

The model equations

To model the fluctuation of the population compartments, we need to derive formulas to express the way they change with respect to time.

The susceptible equation

Let’s consider an initial moment _tₒ. _Each day, an infectious individual spreads the disease to a fraction of the susceptible individuals, which become infectious themselves.

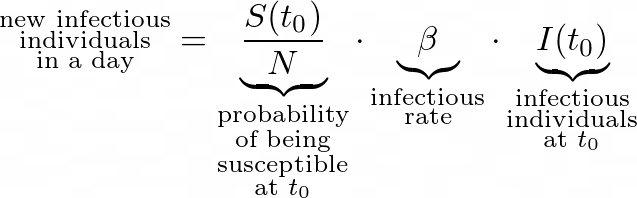
At some moment t, the number of new infectious individuals is:

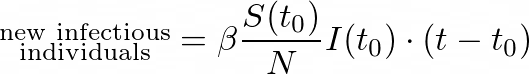
And so, by subtracting the new infectious individuals from the initially susceptible ones, we obtain:

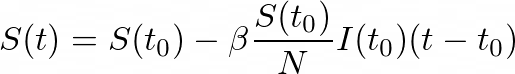
To get the instantaneous rate of change, we divide by (_t- tₒ) _and take the limit as t approaches tₒ:

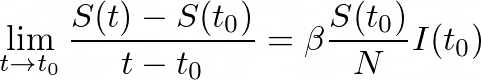
This limit is nothing but the derivative of S with respect to time at some point tₒ. And so:

The infectious equation

Again, let’s consider an initial moment _tₒ. _Each day, new individuals become infectious, and some of the already infectious recover.

We saw previously that:

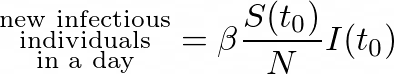
Furthermore,

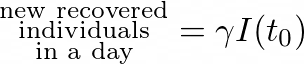
By combining these observations, we can write:

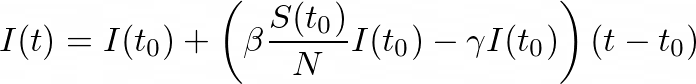
To get the derivative of I, by dividing by (_t- tₒ) _and taking the limit as _t _→ _tₒ, _we get:

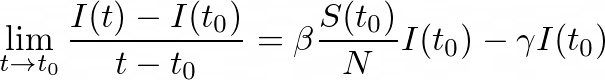
which means that:

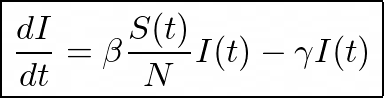
The recovered equation

Same as before, let’s consider an initial moment _tₒ. _Each day, a part of the infectious individuals recover.

We saw that:

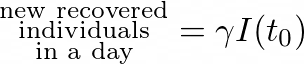
And so

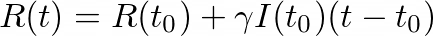
As we did previously, we’ll divide by (_t- tₒ) _and take the limit as _t _→ _tₒ _to get the derivative of R:

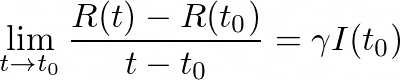
which leads us to:

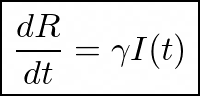
Unifying the model

Putting the three formulas together gives us the SIR model system of ODEs:

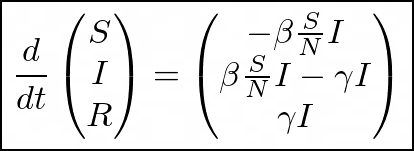
Or, by letting

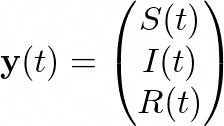
the system becomes:

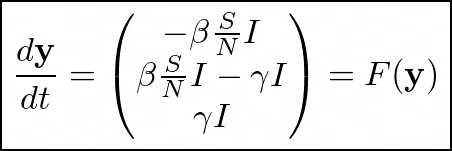
Put in this form, we can simply treat the system as an ODE.

Visualizing the model

We can observe that this system above is non-linear (analytic solutions can, however, be found in an implicit form). Nonetheless, since our purpose is to visualize the model, we’ll resort to a numerical method to solve the system.

The Euler method

The Euler method is a procedure for solving ordinary differential equations numerically given an initial value.

For our case, we’ll consider the number of individuals in each compartment to be known at tₒ = 0:

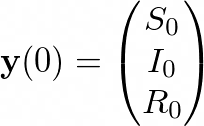
The Euler method consists of iterating through

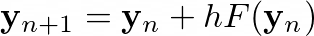
where h is the chosen step. By performing this, we can approximate

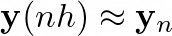
Coding the solution

Let’s write some code to find and plot the solution:

	import numpy as np
	import matplotlib.pyplot as plt
	from matplotlib.animation import FuncAnimation

	class SIR:
	  def __init__(self, beta, gamma, S0, I0, R0):
	    self.beta = beta
	    self.gamma = gamma

	    self.y0 = np.array([S0, I0, R0])
	    self.N = sum(self.y0)

	  def F(self, y):
	    S, I, R = y 
	    return np.array([ -self.beta * I * S / self.N, self.beta * I * S / self.N - self.gamma * I, self.gamma * I])

	  def euler(self, tmax, h):
	    y0 = self.y0
	    t = 0

	    while t <= tmax:
	      y = y0 + h * self.F(y0)
	      yield t, y

	      y0 = y
	      t += h

	  def plot(self, days):
	    X, Y = [], []
	    h = .2

	    for t, y in self.euler(days, h):
	      X.append(t)
	      Y.append(y)

	    fig, ax = plt.subplots()
	    ax.set_xlim(0, days)
	    ax.set_ylim(0, self.N)

	    S_line, = ax.plot(0, 0, color='#4FA1E4')
	    I_line, = ax.plot(0, 0, color='#FE2020')
	    R_line, = ax.plot(0, 0, color='#40D752')

	    def iter(i):
	      S_line.set_xdata(X[:i])
	      I_line.set_xdata(X[:i])
	      R_line.set_xdata(X[:i])

	      Yt = np.transpose(Y[:i])

	      S_line.set_ydata(Yt[0])
	      I_line.set_ydata(Yt[1])
	      R_line.set_ydata(Yt[2])

	      return S_line, I_line, R_line,

	    anim = FuncAnimation(fig, func=iter, frames=range(1, int(days/h)), interval=50, repeat=False)

	    plt.xlabel('Day')
	    plt.ylabel('Population')
	    plt.legend(['Susceptible', 'Infected', 'Recovered'], frameon=False, loc='upper center', ncol=3)
	    plt.title('SIR model')

	    plt.show()

#simulation #mathematical-modeling #visualization #mathematics #differential-equations