Big O notation is a simplified analysis of an algorithm’s efficiency. Big O notation gives us an algorithm’s complexity in terms of input size, N. It gives us a way to abstract the efficiency of our algorithm or code from the machines/computers they run on. We don’t care how powerful our machine is, but rather, the basic steps of the code. We can use big O to analyze both time and space. I will go over how we can use Big O to measure time complexity using Ruby for examples.
Types of measurement
There are a couple of ways to look at an algorithm’s efficiency. We can examine worst-case, best-case, and average-case. When we examine big O notation, we typically look at the worst-case. This isn’t to say the other cases aren’t as important.
General rules
- Ignore constants
5n ->O(n)
Big O notation ignores constants. For example, if you have a function that has a running time of 5n, we say that this function runs on the order of the big O of N. This is because as N gets large, the 5 no longer matters.
2. In the same way that N grows, certain terms “dominate” others
Here’s a list:
O(1) < O(logn) < O(n) < O(nlogn) < O(n²) < O(2^n) < O(n!)
We ignore low-order terms when they are dominated by high order terms.
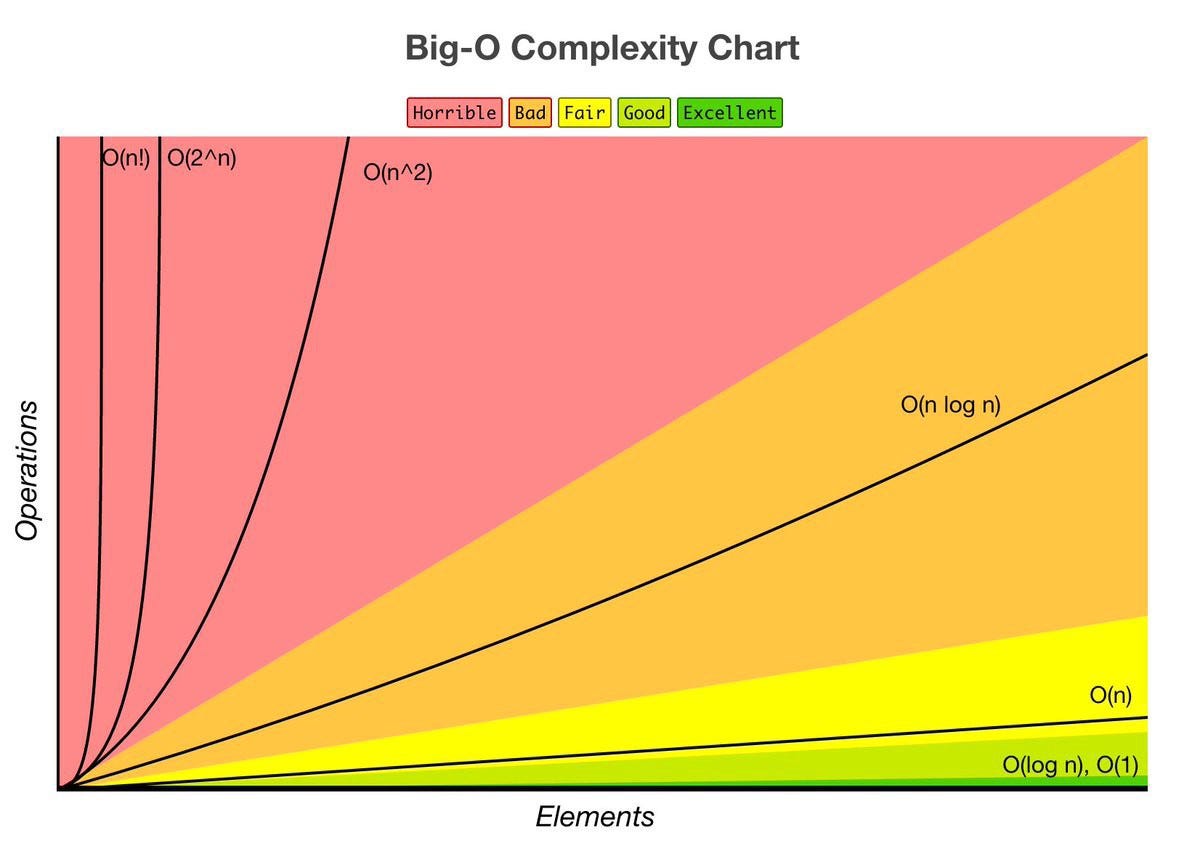
Constant Time: O(1)

This basic statement computes x and does not depend on the input size in any way. This is independent of input size, N. We say this is a “Big O of one” or constant time.
#time-complexity #algorithms #big-o-notation #flatiron-school #algorithms
