One of the most beautiful concepts in statistics and probability is Central Limit Theorem,people often face difficulties in getting a clear understanding of this and the related concepts, I myself struggled understanding this during my college days (eventually mugged up the definitions and formulas to pass the exam). In its core it is a very simple yet elegant theorem that enables us to estimate the population mean. Here I will try to explain these concepts using this toy dataset on customer demographics available on Kaggle (this is a fictional dataset created for educational purposes). Without wasting much time lets dive in and try to understand what CLT is

CENTRAL LIMIT THEOREM

Here is what Central Limit Theorem states

If you take sufficiently large samples from a distribution,then the mean of these samples would follow approximately normal distribution with mean of distribution approximately equal to population mean and standard deviation equal on 1/√n times the population standard deviation (here n is number of elements in a sample)

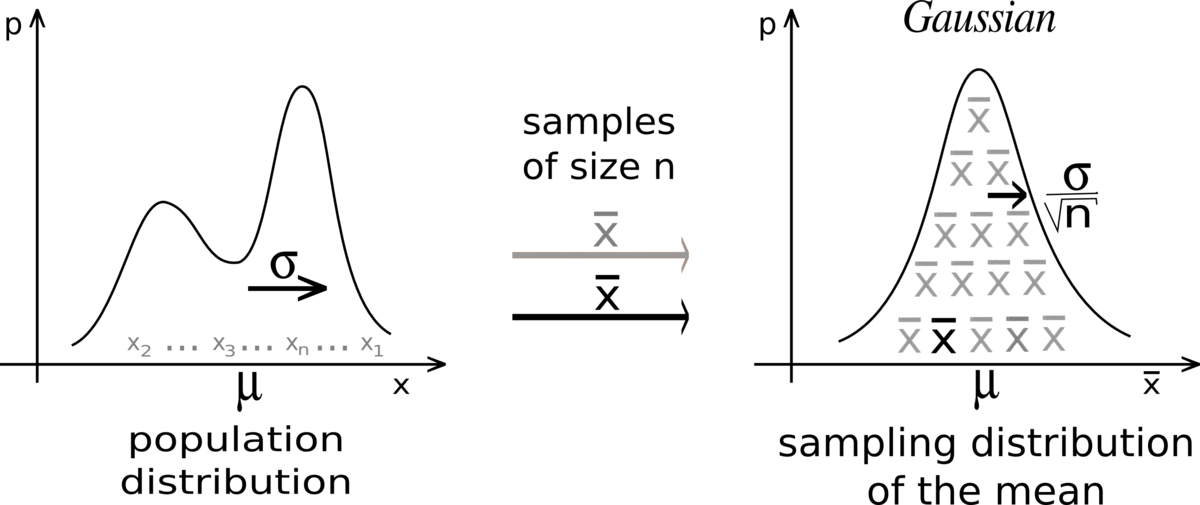
Now comes the fun part, in order to have a better understanding and appreciation of the above statement, let us take our toy dateset (will take the annual income column for our analysis) and try to check if these approximations actually holds true.

We will try to estimate the mean income of a population, first let us have a look at the distribution and size the population

df = pd.read_csv(r'toy_dataset.csv')
print("Number of samples in our data: ",df.shape[0])
sns.kdeplot(df['Income'],shade=True)

Annual Income Distribution of Population (Image By Author)

Well, we can fairly say this is isn’t exactly a normal distribution and the original population mean and standard deviation is 91252.798 and 24989.501 respectively. Now have a good look on to these numbers and let’s see if we could use Central Limit Theorem to approximate these values

#exploratory-data-analysis #central-limit-theorem #data-science #probability #statistics #data analysis