They are parametric generative models that attempt to learn the true data distribution. Hence, once we learn the Gaussian parameters, we can generate data from the same distribution as the source.
We can think of GMMs as the soft generalization of the K-Means clustering algorithm. Like K-means, GMMs also demand the number of clusters K as an input to the learning algorithm. However, there is a key difference between the two. K-means can only learn clusters with a circular form. GMMs, on the other hand, can learn clusters with any elliptical shape.
Also, K-means only allows for an observation to belong to one, and only one cluster. Differently, GMMs give probabilities that relate each example with a given cluster. In other words, it allows for an observation to belong to more than one cluster — with a level of uncertainty. For each observation, GMMs learn the probabilities of that example to belong to each cluster k.
In general, GMMs try to learn each cluster as a different Gaussian distribution. It assumes the data is generated from a limited mixture of Gaussians.
Assuming one-dimensional data and the number of clusters K equals 3, GMMs attempt to learn 9 parameters.
- 3 parameters for the means
- 3 parameters for the variances
- 3 scaling parameters
Here, each cluster is represented by an individual Gaussian distribution (for this example, 3 in total). For each Gaussian, it learns one mean and one variance parameters from data. The 3 scaling parameters, 1 for each Gaussian, are only used for density estimation.
To learn such parameters, GMMs use the expectation-maximization (EM) algorithm to optimize the maximum likelihood. In the process, GMM uses Bayes Theorem to calculate the probability of a given observation xᵢ to belong to each clusters k, for k = 1,2,…, K.
Let’s dive into an example. For the sake of simplicity, let’s consider a synthesized 1-dimensional data. But, as we are going to see later, the algorithm is easily expanded to high dimensional data with D > 1. You can follow along using this jupyter notebook.
To build a toy dataset, we start by sampling points from K different Gaussian distributions. Each one (with its own mean and variance) represents a different cluster in our synthesized data. To make things clearer, let’s use K equals 2.
Below, you can see the resulting synthesized data. We are going to use it as training data to learn these clusters (from data) using GMMs. Note that some of the values do overlap at some point.

We can think of GMMs as a weighted sum of Gaussian distributions. The number of clusters K defines the number of Gaussians we want to fit.
As we said, the number of clusters needs to be defined beforehand. For simplicity, let’s assume we know the number of clusters and define K as 2. In this situation, GMMs will try to learn 2 Gaussian distributions. For 1-dim data, we need to learn a mean and a variance parameter for each Gaussian.
Before we start running EM, we need to give initial values for the learnable parameters. We can guess the values for the means and variances, and initialize the weight parameters as 1/k.
Then, we can start maximum likelihood optimization using the EM algorithm. EM can be simplified in 2 phases: The E (expectation) and M (maximization) steps.
In the E step, we calculate the likelihood of each observation xᵢ using the estimated parameters.
1-d gaussian distribution equation
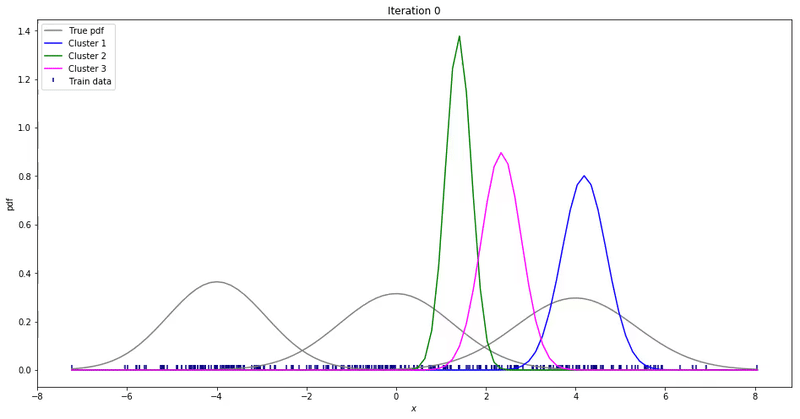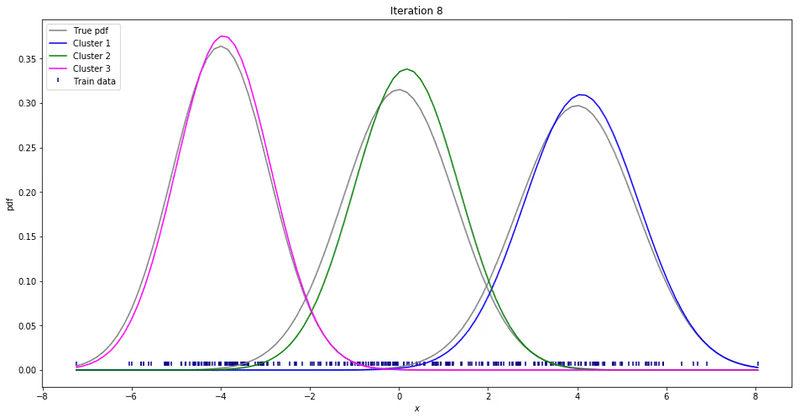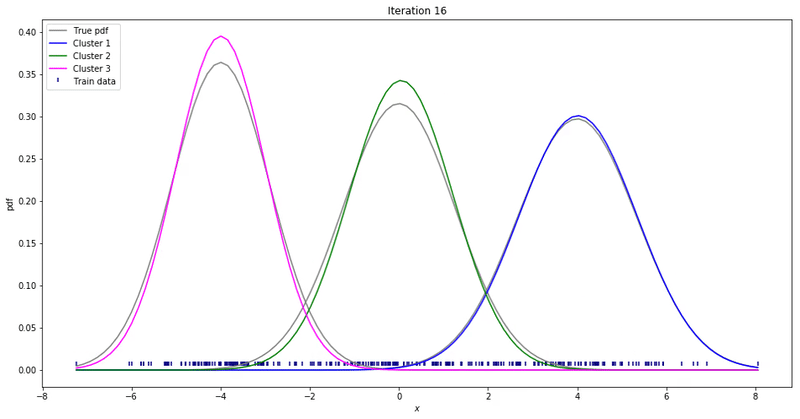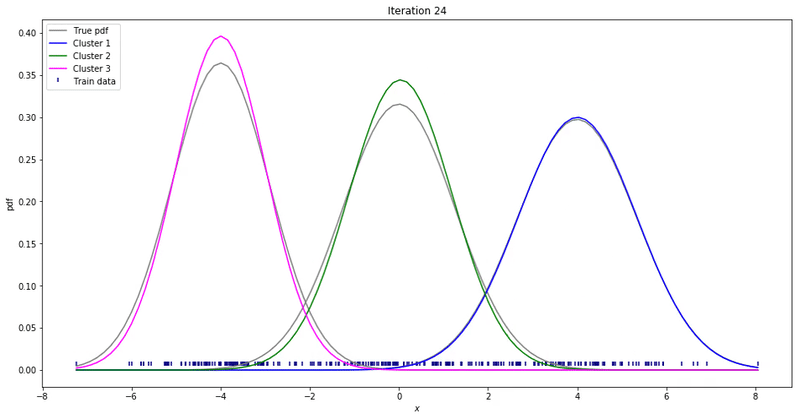
For each cluster k = 1,2,3,…,K, we calculate the probability density (pdf) of our data using the estimated values for the mean and variance. At this point, these values are mere random guesses.
Then, we can calculate the likelihood of a given example xᵢ to belong to the kᵗʰ cluster.
Using Bayes Theorem, we get the posterior probability of the kth Gaussian to explain the data. That is the likelihood that the observation xᵢ was generated by kᵗʰ Gaussian. Note that the parameters Φ act as our prior beliefs that an example was drawn from one of the Gaussians we are modeling. Since we do not have any additional information to favor a Gaussian over the other, we start by guessing an equal probability that an example would come from each Gaussian. However, at each iteration, we refine our priors until convergence.
Then, in the maximization, or M step, we re-estimate our learning parameters as follows.
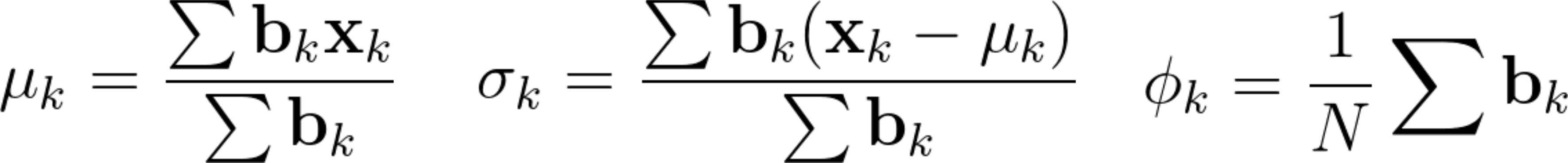
Here, for each cluster, we update the mean (μₖ), variance (σ₂²), and the scaling parameters Φₖ. To update the mean, note that we weight each observation using the conditional probabilities bₖ.
We may repeat these steps until converge. That could be up to a point where parameters’ updates are smaller than a given tolerance threshold. At each iteration, we update our parameters so that it resembles the true data distribution.
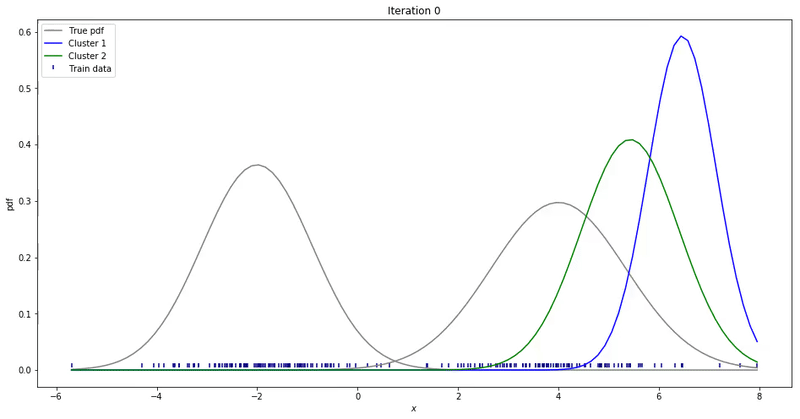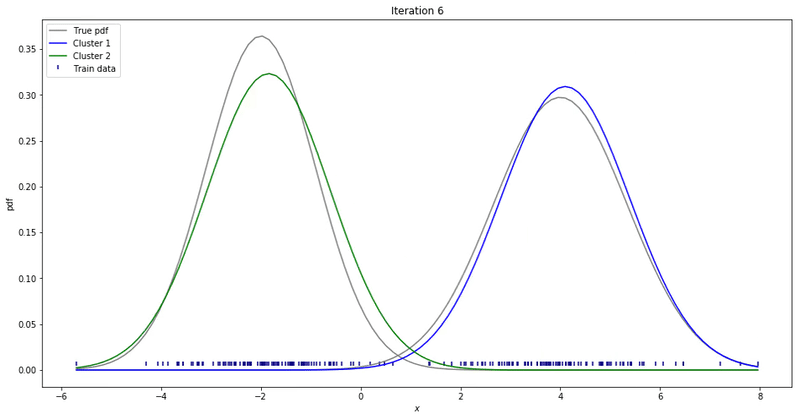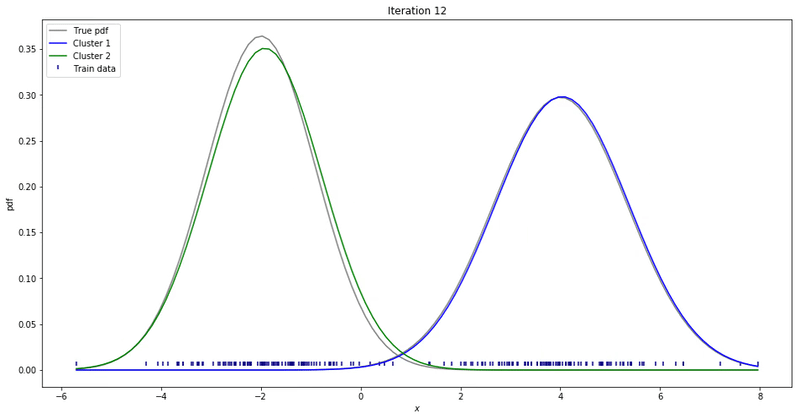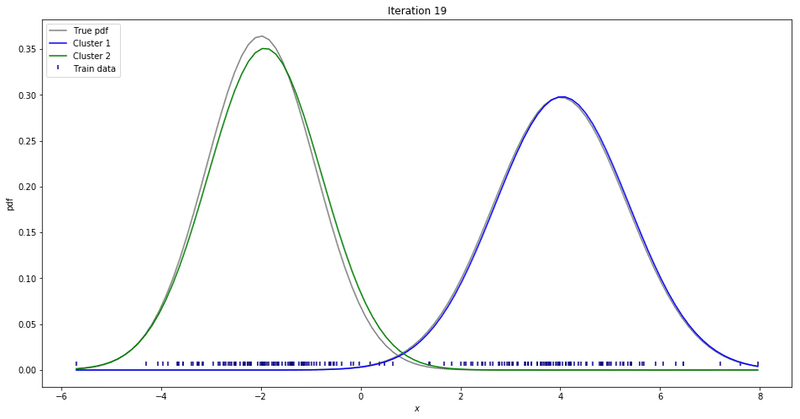
Gaussian Mixture Models for 1D data using K equals 2
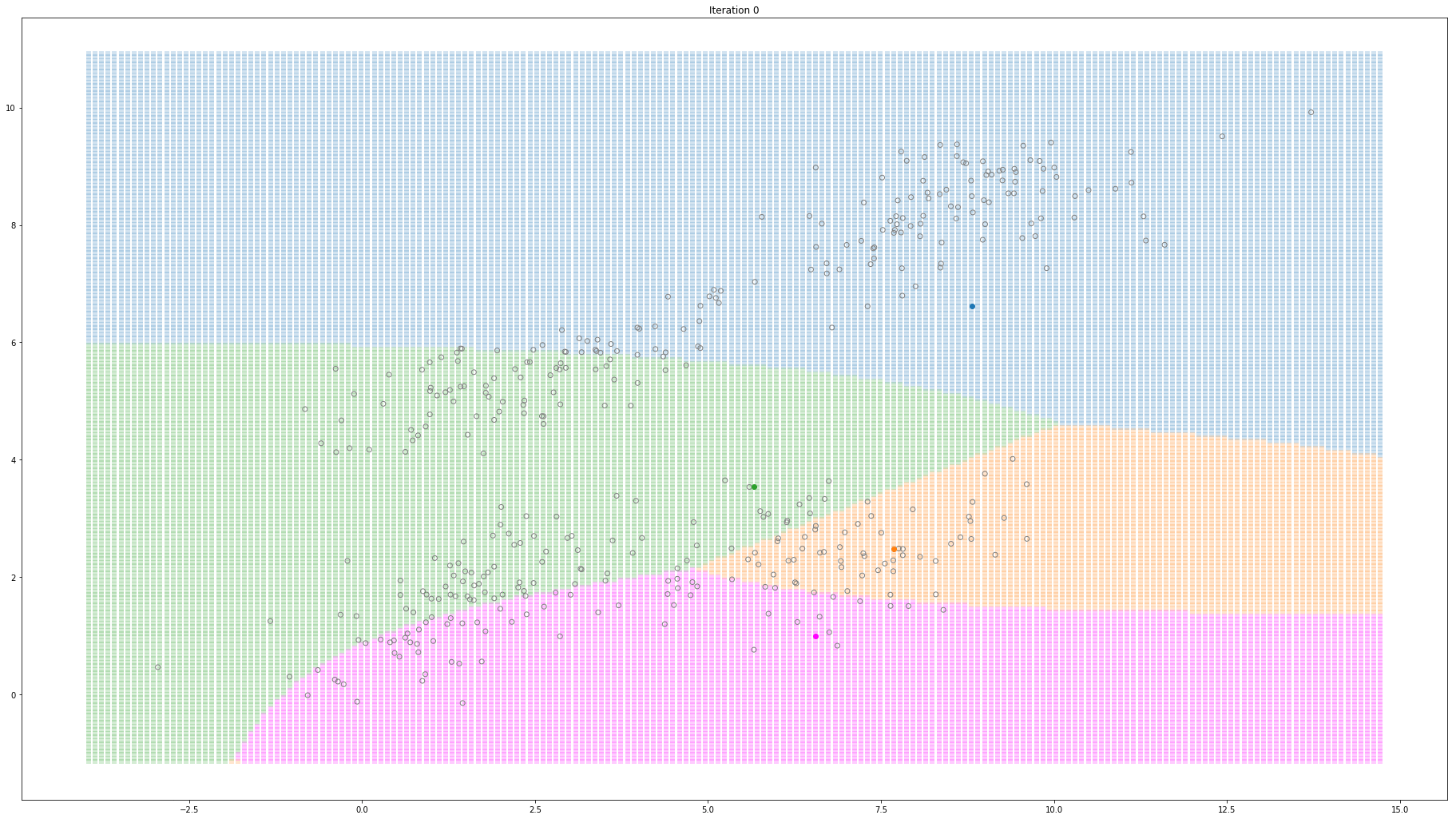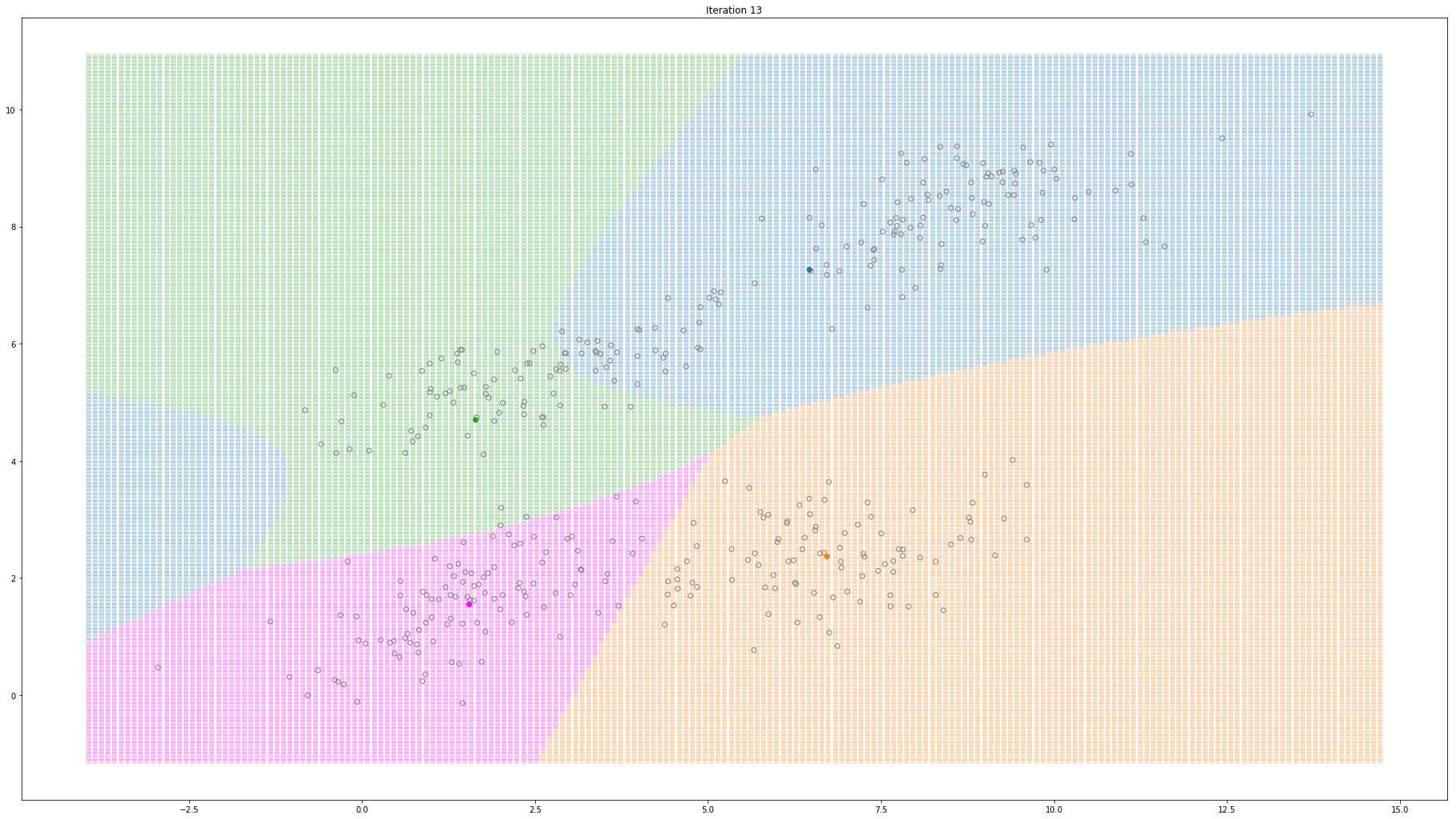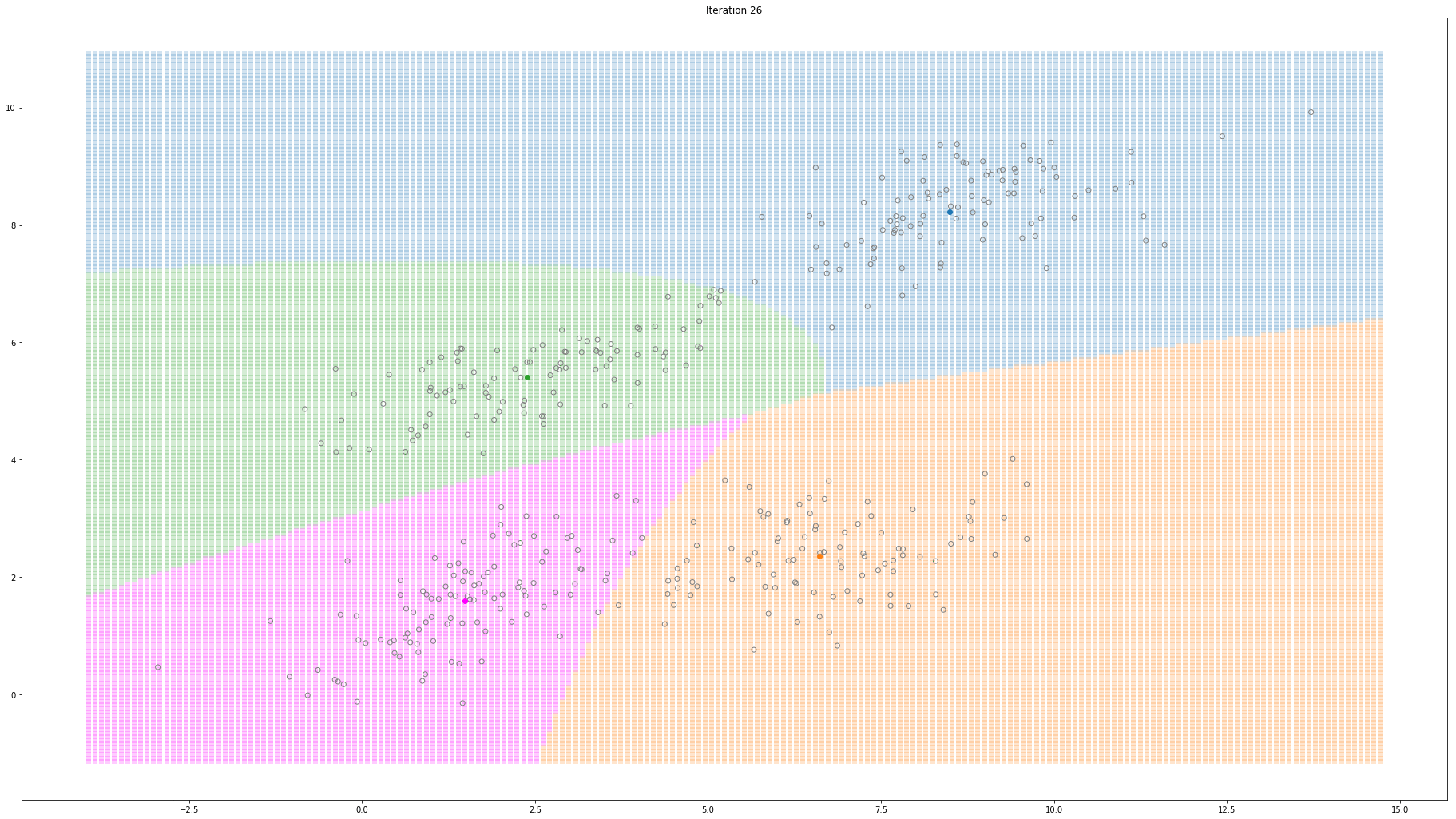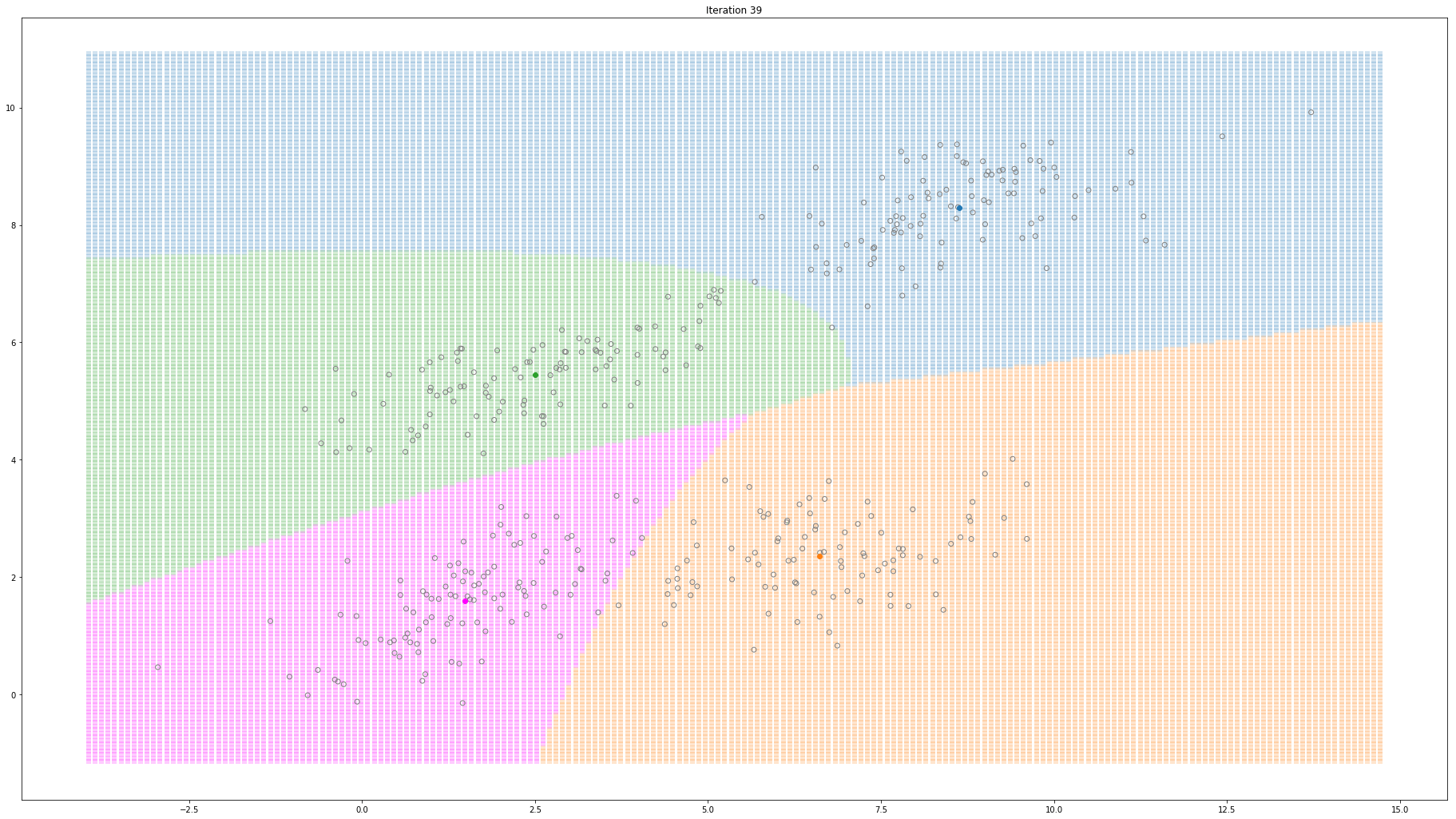
For high-dimensional data (D>1), only a few things change. Instead of estimating the mean and variance for each Gaussian, now we estimate the mean and the covariance. The covariance is a squared matrix of shape (D, D) — where D represents the data dimensionality. Below, I show a different example where a 2-D dataset is used to fit a different number of mixture of Gaussians.
Check the jupyter notebook for 2-D data here.
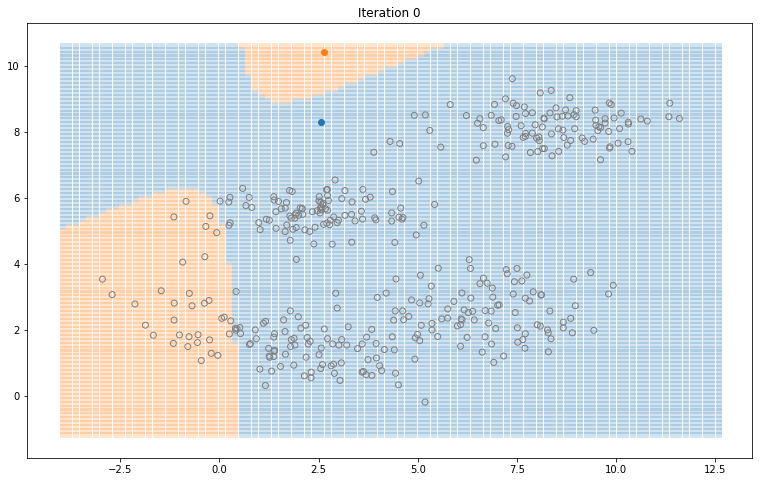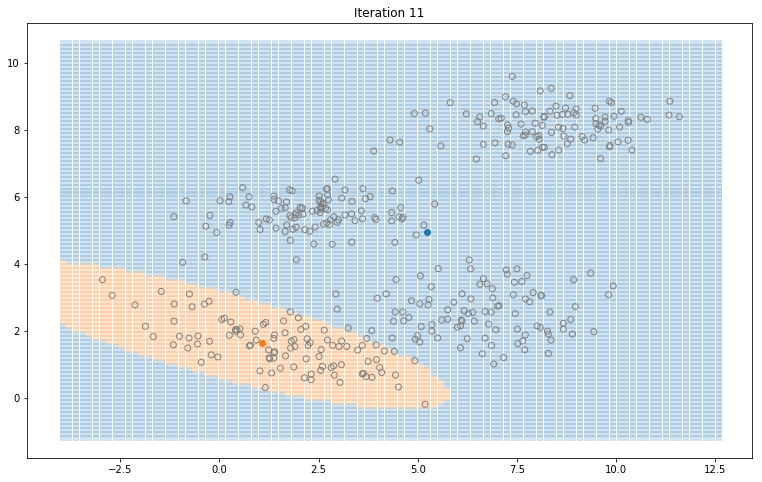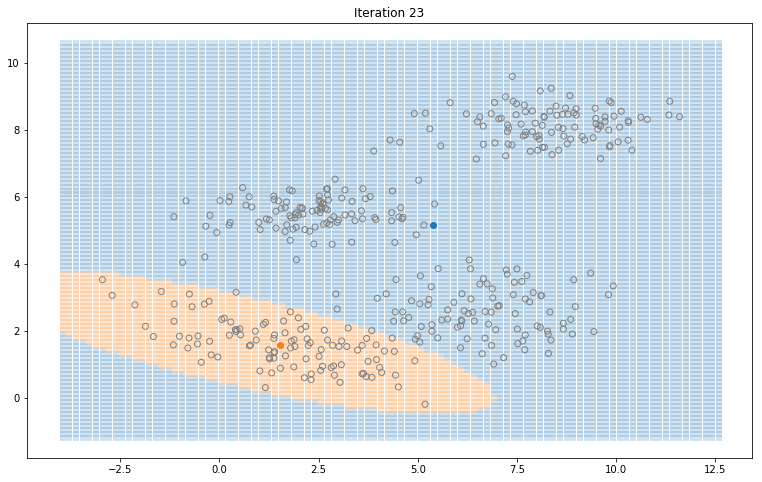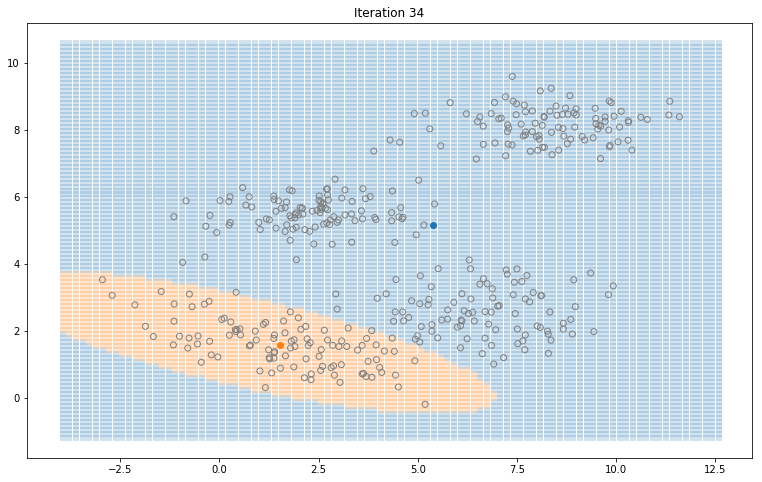
Gaussian Mixture Models for 2D data using K equals 2

Gaussian Mixture Models for 2D data using K equals 3

Gaussian Mixture Models for 2D data using K equals 4
Note that the synthesized dataset above was drawn from 4 different gaussian distributions. Nevertheless, GMMs make a good case for two, three, and four different clusters.
That is it for Gaussian Mixture Models. These are some key points to take from this piece.
- GMMs are a family of generative parametric unsupervised models that attempt to cluster data using Gaussian distributions.
- Like K-Mean, you still need to define the number of clusters K you want to learn.
- Different from K-Means, GMMs represent clusters as probability distributions. This allows for one data points to belong to more than one cluster with a level of uncertainty.
Thanks for reading.
Originally published by Thalles Silva at towardsdatascience.com
============================================
Thanks for reading :heart: If you liked this post, share it with all of your programming buddies! Follow me on Facebook | Twitter
Learn More
☞ Learn NumPy Arrays With Examples
☞ Neural Network Using Python and Numpy
☞ Deep Learning Prerequisites: The Numpy Stack in Python
#python #machine-learning #data-science