Abbreviated as SVM, support vector machine learning algorithm is commonly used for classification problems. It gives us a better way to understand a non-linear decision boundary.

Let’s begin by considering a scenario where one might want to classify the following data —

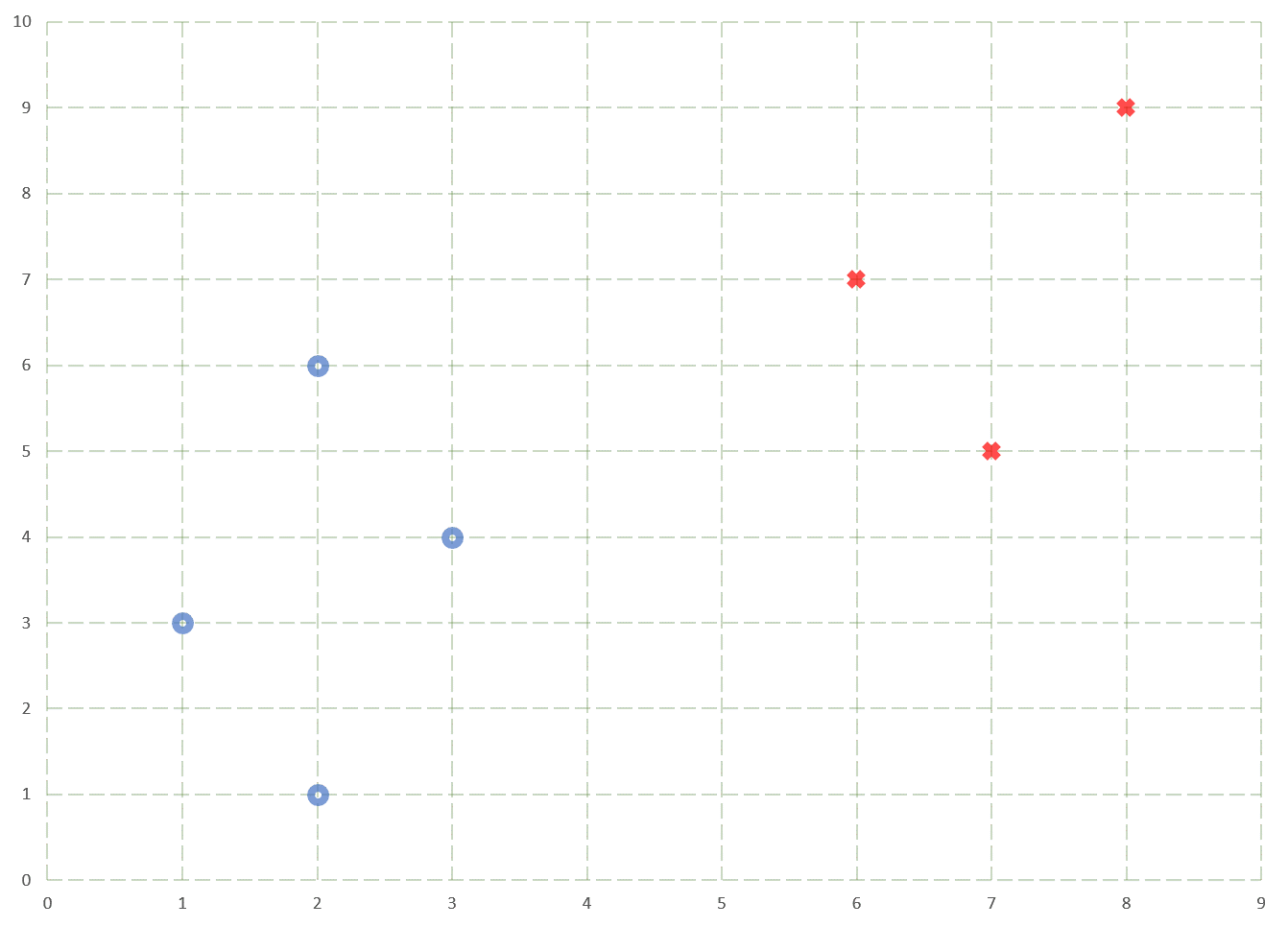
Data set used to illustrate a simple SVM model.

It is quite evident that the data can be separated into their respective classes using a simple linear decision boundary. However, there are multiple such decision boundaries that can be used to separate the two classes. In fact, there are an infinite number of linear decision boundaries that can be drawn to separate the red and the blue class. Consider the following decision boundaries —

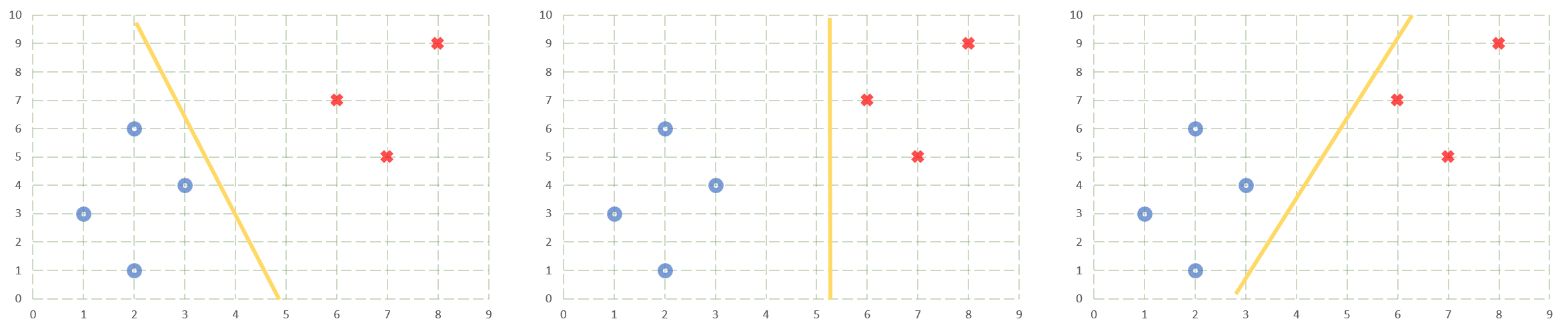
Possible decision boundaries that can be used to classify the data.

• The one on the left is too close to the blue class implying “whenever in doubt classify the point to be red”.
• The decision boundary in the middle graph is closer to the red class. The decision boundary being close to the red class implies that if a model classifies a point as being red then it is more sure of its decision had it classified the same point as being blue, thereby following “whenever in doubt classify the point as blue”. Also, intuition says we can do better than a perfectly straight decision boundary.
• In the last graph, the decision boundary is close to the instances of both the red and the blue classes.

From the above discussion, we may conclude that we want a decision boundary that is not too close to either of the two classes. To help us find such a line, SVM is used.

Support vector machine learning algorithm concentrates on those points of both the classes that are close to each other. The idea being that if a classifier does a good job of classifying challenging points it is likely to perform better on the data. SVM does this by looking up for the closest points from both the classes called the **support vectors. **Once SVM has found its support vectors it will try to find a line that is at maximal distance from these points. In case of two points the perpendicular bisector is the line that is equidistant and therefore at maximal distance from the two points. Any other line will be closer to one point than the other one.

We can also say that given the support vectors and multiple lines we will choose that line as our decision boundary whose distance is as large as possible from all support vectors.

#machine-learning #data-science #support-vector-machine