The laws of nature are complicated and throughout time, Scientists from all corners of the world have attempted to model and reengineer what they see around them to extract some value from it. Quite often we see a pattern that comes up time and time again: be it the golden ratio, or be it that fractal spiral.

In its empirical form, the Power Law describes how a lot of the time, not much actually happens but more often than not, some patterns cover a wide range of magnitudes. Think about the following relatable examples:

1. Number of Comments on a Post
2. Number of Social Media Followers
3. Money Grossed at Box Offices
4. Books sold for Top Authors
5. Market Capitalisation of American Companies

They all seem to fit the pattern, but we can also see these examples widely in the form of natural phenomena:

1. Ratio of Surface Area to Volume
2. Fractal Geometry
3. Initial Mass Function of Stars
4. Distribution of Wealth

There are plenty more of these examples but the thing that really begs the question is, what is actually driving this skewed phenomena? Why is there a lot of density at low values and why, at other times, do we get incidences at really far ends of the tail?

Let’s first cover the mathematics of the it, before discussing it more in detail.

---

Probability Distribution of Power-Laws

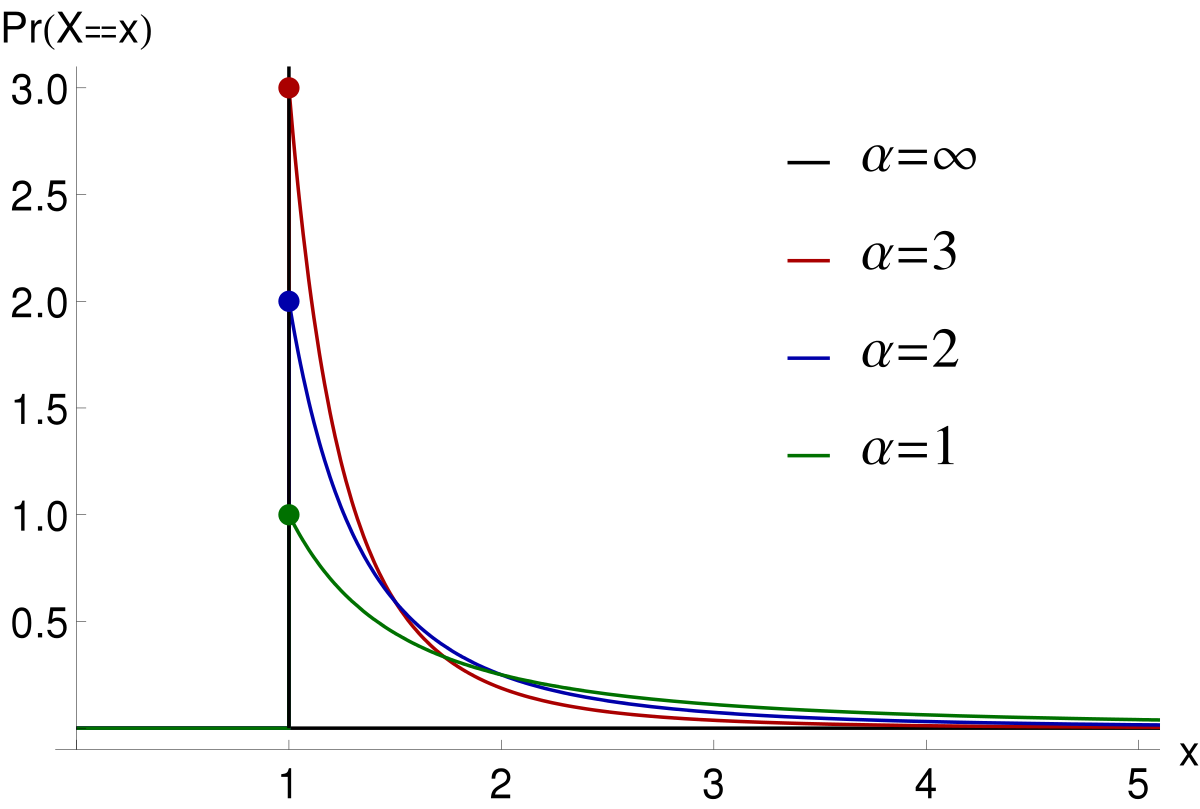
A random variable that characterises a power-law Distribution can be defined as follows:

where C is the normalisation constant C=(a-1)x^α-1. This equation only really makes sense if α>1, but as a more compact form, we can also write it as follows:

Note that from this functional form, we can see that if we apply a logarithmic function, the functional form becomes linear:

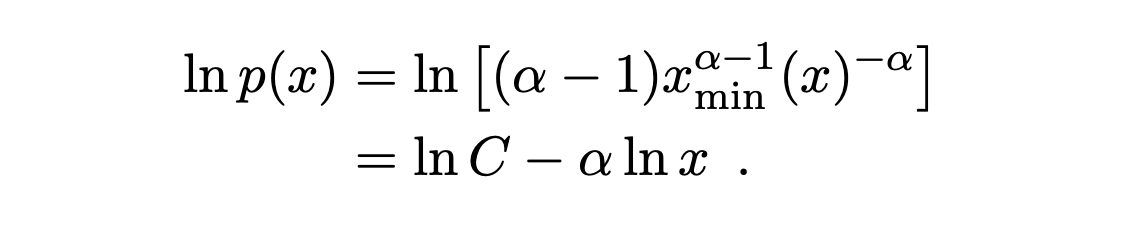
Scale Invariance of Power Law Distributions

So if we compare the densities at p(x) and at some other p(c x), where c is a constant, we find that they’re always proportional. That is, p(c x) ∝ p(x). This behaviour shows us that the relative likelihood between small and large events is the same, no matter what choice of “small” we make.

#artificial-intelligence #mathematics #data-science #data analysis