What’s this about
- First I’ll talk about what made me curious about how Eigenvalues are actually computed.
- Then I’ll share my implementation of the simplest algorithm (QR method) and do some benchmarking.
- Lastly, I’ll share how you can animate the steps the algorithm goes through to finds the Eigenvectors!
They’re Everywhere
Eigenvalues and eigenvectors can be found all over mathematics, and especially applied mathematics. Statistics, Machine Learning, Data Science all fall into that bucket.
Some time ago I decided to learn Rcpp and C++ by implementing Principal Component Analysis (PCA). I knew that the solution to the PCA problem was the eigenvalue decomposition of the Sample Variance-Covariance Matrix. I realized that I would need to write my own version of the built-in eigen function in C++ and that is when I realized that beyond a 2x2 case, I didn’t know how eigen actually works. What I discovered was the QR Method that I read about here.
Why n > 2 is different
With a 2x2 matrix, we can solve for eigenvalues by hand. That works because the determinant of a 2x2 matrix is a polynomial of degree 2 so we can factorize and solve it using regular algebra. But HOW do you compute eigenvalues for large matrices? Turns out, that when you can’t factorize and solve polynomials, what you really should be doing is factorizing matrices. By pure coincidence, the Numberphile YouTube channel recently had a video on this idea posted here. Worth checking out if you are into this type of content!
Quick Refresher: What are they?
First, just a quick refresher on what Eigenvalues and Eigenvectors are. Take a square matrix X. If there is a vector v and a scalar λ such that
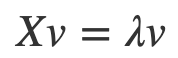
then v is an eigenvector of Xand λ is the corresponding eigenvalue ofX.
In words, if you think of multiplying v by X as applying a function to**v**, then for this particular vector v this function is nothing but a stretching/squishing scalar multiplication. Usually multiplying a vector by a matrix equates to taking linear combinations of the components of a vector. But if you take an Eigenvector, you don’t need to do all that computation. Just multiply by the Eigenvalue and you are all good.
Computing: The QR Method
The QR method for computing Eigenvalues and Eigenvectors begins with my beloved QR matrix decomposition. I wrote about it in my previous post. This decomposition allows one to express a matrix X=QR as a product of an orthogonal matrix **_Q _**and an upper triangular matrix R. Again, the fact that **_Q _**is orthogonal is important.
The central idea of the QR method for finding the eigenvalues is iteratively applying the QR matrix decomposition to the original matrix X.
Similar Matrices
Here I need to mention one mathematical property of Eigenvalues of X. If we take any invertible matrix M then the matrix
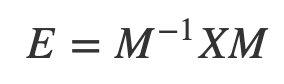
will have the same Eigenvalues as X. Such matrices E and X are formally defined as similar matrices, which simply means that they have the same Eigenvalues. Eigenvectors will be different, however. Also, recall that the Q in QR is orthogonal and therefore inevitable.
QR Algorithm
So, the idea of the QR method is to iterate the following steps
- Apply QR decomposition to**_ X_** so that
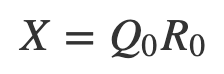
2. Let
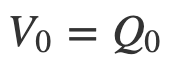
and compute
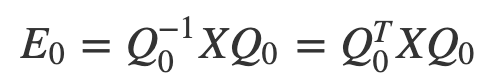
Note: E is similar to X. Their Eigenvalues are the same.
3. Then decompose
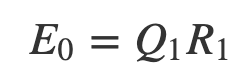
4. And so
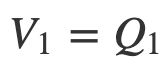
and
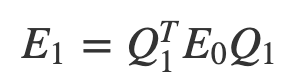
5. Iterate unit the ith E is essentially diagonal.
When **_E _**is diagonal what you have are the desired Eigenvalues on the diagonal, and V are the Eigenvectors!
This is the simplest version of the **_QR method. _**There are a couple of improved versions that I will not go into, but you can read about them here.
Next, I want to write a function in R and C++ to implement the method and verify for me that it works.
#r #data-visualization #mathematics #linear-algebra #data-science #data analysis
