Introduction
This article is meant to be a gentle introduction into formal language theory. As with everything, we will try to balance mathematical rigour with concrete examples that have linguistically motivated examples.
Topics to touch on:
- Elementary formal language theory
- Regular languages
- Regular expressions
- Languages
- Finite state automata
- Regular relations
Basic Notions
Sets and Elements
Formal languages are defined to have a certain, specific alphabet. The alphabet may be denoted by ∑.

This alphabet set, consists of elements called letters. This set is a finite set. Each letter is a symbol that can be from “abc…”, “123…”. Symbols can even be words.
A sequence of letters may be called a word or a string.
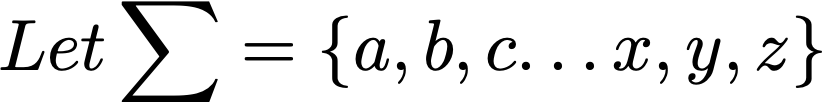
Then these are examples of string:
- Cat
- Arachnadiscoteka
- ASKdnskjf
- uuuuuuu
- Ouuuuu
- ksdjfnskdjfnSOULJABOITELLEMksjdnfksjdnf
Length of a String
The length of a string, or the number of characters in a string, is denoted by |w|.
Empty String
We consider the empty string of 0 length as unique and denote by ϵ.
Concatenation Operation
Concatenation, is the addition of 2 strings together, where order matters. For example, “artificial” + “intelligence” = “artificialintelligence”. Given:


Concatenation is denoted by:

Note that:

For every string w:
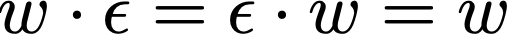
Some examples:
- “learn”+”s”
- “learn”+”ed”
- “learn”+”ing”
Exponent Operation
For every string w:
- w⁰=ϵ
For all exponents n>0:
- wⁿ=wⁿ⁻¹ ⋅ w
For example:
If w=”go”, then:
- w⁰=ϵ=””
- w¹=w=”go”
- w²=w*w=”gogo”
- w³=www=”gogogo”
Reversal Operation
If w is a string, then reverse of w is:
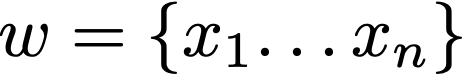

Palindrome is defined by:
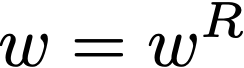
Here we mean words like “ana”, “anna”, “racecar” etc. I’m not sure if these are technically called symmetry. But everyone would understand exactly what I mean if I called these words symmetric. If there is such a concept as symmetry in formal language theory, I wonder how it would connect to Group Theory.
Coincidentally, group theory arises out of our need to study symmetry of geometrical objects and spaces. Where we might build out the theory exactly the same way that formal language theory is built, using sets as the objects then defining standard operations.
On this later…
Substring Set, or String Sub Set
If w is a string, then a substring of w is a sequence formed by taking a contiguous symbols of w in the order in which they occur in w.
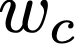
is a substring of w if and only if there are 2 other substring such that

Also w₁ and wᵣ may be empty strings. These two substring are special cases of substrings called, prefix and suffix.
#naturallanguageprocessing #deep-learning #machine-learning #linguistics #deep learning
