Today we will be reviewing the heap data structure.

A heap is a tree-based data structure, which indicates a heap will have a root node and some child nodes. We usually work with the binary heap. A binary has a left child and a right child. The following image is an example of a heap data structure.

Heap data structure.

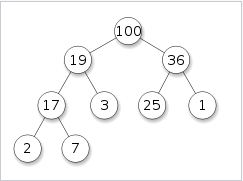
To insert a node into a heap, we use the push function, and to remove the root from the heap, we use the pop function. When a new node needs to be inserted, it is inserted at the end of the heap structure. When we pop from a heap structure, the root element is removed from the heap structure. Once the root is removed, restructure is necessary to preserve the structure of the heap.

If we want to represent our heap in form of an array, index ‘k’ will hold the root node, then its left child is stored at index ‘2k + 1’ and its right child at index ‘2k + 2’.

The above heap will be represented as follows:

Array representation of Heap

Based on our requirement, we can either have a min-heap or a max-heap.

What is the difference between min-heap and max-heap?

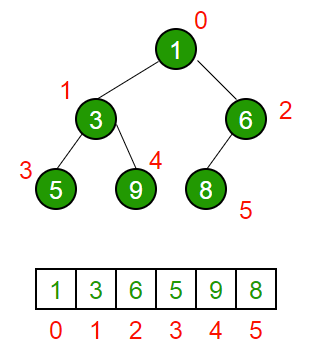
In min-heap, the root nodes will be smaller than the child nodes.

An example of min-heap is as follows:

Min Heap

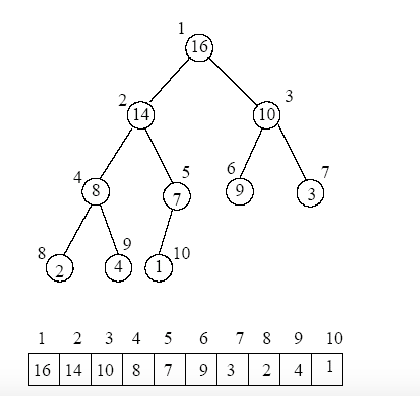
In a max-heap, the root node will be greater than the child node.

An example of max-heap is as follows:

Max Heap

Why would we require a min-heap or a max-heap?

Sorting is one of the applications of the heap. When we create a min-heap or a max-heap, it is easy for us to arrange our elements in ascending or descending order.

What are the other applications of the heap?

1. We can create a priority queue using a heap. In a priority queue, each element will have a priority associated with it. Based on this priority we can determine the position of elements in the queue.
2. We can get Kth largest/smallest element in our array.

Let us move into sorting.

To perform heapsort we need to follow 2 steps.

1. Build heap — Building heap is a method to create a tree-like data structure from the unsorted input array.
2. Heapify — It is similar to building heap, but assumes that the tree is sorted partly.

Algorithm:

1. We build the heap as our first step, call heapify, and keep track of the current root.
2. The left child of the root is 2i+1 where i is the root index and the right child of the root is 2i+2.
3. Since we are building max heap, our root should be greater than the child. Exchange the position of the children with root if the root is smaller than the children.
4. Once the max-heap is built, remove the root node and place it at the end of the array.

#coding #programming #python #heapsort #365dayschallenge